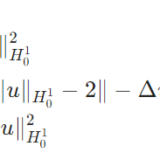どうも、木村(@kimu3_slime)です。
今回は、コンパクト作用素は有界作用素であることの証明を紹介します。
定義の確認
\(X,Y\)をノルム空間、\(F:X \to Y\)を写像とします。
\(F\)がコンパクト作用素とは、\(X\)の任意の有界集合\(A\)について、その像の\(Y\)における閉包\(\mathrm{Cl}_Y (F(A))\)がコンパクトとなることです。
\(F\)がコンパクト作用素であることの同値な条件として、「\(X\)の任意の有界な点列\((u_n)\)に対し、\((F(u_n))\)が\(Y\)において収束する部分列を持つ」が知られています。
\(F\)が有界作用素とは、「すべての\(u \in X\)に対し\(\|F(u)\|_Y \leq M \|u\|_X\)」を満たすような\(M\)が存在することです。
証明
対偶として、\(F\)が有界作用素でないならば、コンパクト作用素でないことを示しましょう。
有界作用素の定義の否定から、すべての\(n \in \mathbb{N}\)に対し、\(\|F(u_n)\|_Y > n \|u_n\|_X\)を満たす\(u_n \in X\)が存在します。
\(u_n =0\)と仮定すると、\(F\)の線形性とノルムの正定値性から\(0=\|F(u_n)\|_Y > n \|u_n\|_X=0\)と矛盾するので、\(u_n\neq 0\)です。
そこで\(v_n := \frac{1}{\|u_n\|_X}u_n\)とします。\(\|v_n\|= \frac{1}{\|u_n\|_X}\|u_n\|_X =1\)なので、\((v_n)\)は\(X\)の有界な点列です。
\(F\)の線形性とノルムの正定値性から、
\[\begin{aligned} & \|F(v_n)\|_Y\\ &= \|\frac{1}{\|u_n\|_X} F(u_n)\|_Y\\ &= \frac{1}{\|u_n\|_X}\|F(u_n)\|_Y \\ & > \frac{1}{\|u_n\|_X} n\|u_n\| \\ &= n\end{aligned}\]
です。どんな部分列\((F_c{n_k})\)を考えても、\(\|F(v_{n_k})\|_Y > n_k\)なので、\(k \to \infty\)で無限大に発散します。したがって、\((F(v_n))\)は収束する部分列を持ちません。
よって、\(F\)はコンパクト作用素ではありません。対偶により、コンパクト作用素は有界作用素であることが示せました。
有界作用素でないと仮定して不都合な点列を作る議論は、有界でないならば連続でないことを示す議論と似ていますね。
逆は一般には成り立たない
有界作用素は、コンパクト作用素とは限りません。
数列空間\(X=Y=\ell^2\)における、恒等作用素\(F= I \)を考えましょう。
\(I(a)=a\)なので、\(\|I(a)\|_ \ell^2= \|a\|_\ell^2\)となるため、\(I\)は有界作用素です。
しかし、\(X\)の単位球面\(B\)を考えます。これは有界な集合です。その像は\(I(B)=B\)で、単位球面は閉集合なので閉包に一致します。\(\ell^2\)における単位球はコンパクトでないので、\(B\)はコンパクトではありません。よって、\(I\)はコンパクト作用素ではありません。
以上、コンパクト作用素は有界作用素であることの証明を紹介してきました。
コンパクト作用素は固有値の議論をするのに都合が良いですが、それは有界作用素の一種として捉えられることがわかりますね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Evans, Lawrence C.(著)
¥16,299 (2022-08-19時点)
こちらもおすすめ
l^2、無限次元ヒルベルト空間の単位球がコンパクトでないことの証明