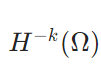どうも、木村(@kimu3_slime)です。
今回は、ポアンカレの不等式とは、証明、\(H_0^1\)ノルムへの応用を紹介します。
ポアンカレの不等式
境界で0のソボレフ空間\(H_0 ^1\)における関数\(u\)のノルムは、その(弱微分の意味での)勾配\(\nabla u\)のノルムで抑えられるという主張が、ポアンカレの不等式(Poincare’s ineuality)です。
\(\Omega \subset \mathbb{R}^N\)を一方向に有界、例えば「\(x \in \Omega\)に対し、\(|x_1| \leq d\)」を満たす\(d\)が存在するとしましょう。このとき、「すべての\(u \in H_0 ^1(\Omega) \)に対し、\(\|u\|_{L^2} \leq C \|\nabla u\| _{L^2}\)」を満たす\(C\)が存在します。
\(\Omega\)(全体)が有界ならば、一方向に有界でもあるので、ポアンカレの不等式は成り立ちます。
証明
\(H_0 ^1\)の定義から、\(C_c ^\infty (\Omega)\)がその稠密な部分集合なので、まずは\(u \in C_c ^\infty\)として示しましょう。
\(x_1\)について部分積分し、\(L^2\)内積についてコーシー・シュワルツの不等式を用います。境界での値が0になっているため、境界の項が消えることに注意しましょう。
\[\begin{aligned} & \|u\|^2_{L^2}\\ &= \int_\Omega |u(x)|^2 dx \\&=|-\int_{\Omega} x_1 \frac{\partial }{\partial x_1} |u(x)|^2 dx |\\&= |-\int_\Omega x_1 (2 u(x) \frac{\partial u}{ \partial x_1}) dx |\\ &\leq 2d| \int_{\Omega} u(x) \frac{\partial u}{ \partial x_1} dx |\\&= 2d |\langle u, \frac{\partial u}{\partial x_1} \rangle_{L^2}| \\ & \leq 2d \|u\|_{L^2} \|\frac{\partial u}{\partial x_1}\|_{L^2} \\ & \leq 2d \|u\|_{L^2} \|\nabla u\|_{L^2}\end{aligned}\]
\(u=0\)のときはどんな定数でも成り立つので、\(u \neq 0\)のとき、\(\|u\|_{L^2}\)で両辺を割れば
\[\|u\|_{L^2} \leq 2d \|\nabla u\|_{L^2}\]
が示せました。\(C:= 2d\)は\(u\)に依存しません。
一般に、\(u \in H_0^1\)としましょう。\(C_c ^\infty (\Omega)\)の稠密性から、点列\((u_n) \subset C_c ^\infty\)で、\(\lim_{n\to \infty} \|u_n -u\|_{H^1}=0\)を満たすものが存在します。特に、\(\lim_{n\to \infty} \|u_n -u\|_{L^2}=0\)かつ\(\lim_{n\to \infty} \|\nabla u_n -\nabla u\|_{L^2}=0\)です。さきほど示した結果から、
\[\|u_n\|_{L^2} \leq 2d \|\nabla u_n\|_{L^2}\]
が成り立ち、極限を取ると不等式は保たれるので、
\[\|u\|_{L^2} \leq 2d \|\nabla u\|_{L^2}\]
が成り立つことが示せました。
まとめれば、\(u\)のノルムの評価をするときに、部分積分によって微分の評価に変え、出てくる\(x_1\)を\(\Omega\)の一方向の有界性で抑える、という方法ですね。
\(H_0 ^1\)ノルムへの応用
\(H^1\)のノルムとは、1階までの弱微分のノルムの和
\[\|u\|_{H^1} = (\sum_{0 \leq |\alpha| \leq 1} \|D^{\alpha} u\|_{L^2}^2)^\frac{1}{2}\]
のことでした。ポアンカレの不等式が成り立つときは、\(H_0^1\)に新たなノルム
\[\begin{aligned} \|u\|_{H_0^1}&: = (\sum_{ |\alpha| = 1} \|D^{\alpha} u\|_{L^2}^2)^\frac{1}{2}\\&= (\sum_{k=1}^N \|\frac{\partial u}{\partial x_k}\|_{L^2}^2)^\frac{1}{2}\\&= (\int_{\Omega} \sum_{k=1}^N |\frac{\partial u}{\partial x_k}(x)|^2 dx)^\frac{1}{2} \\ &=(\int_{\Omega} |\nabla u(x)|^2 dx)^\frac{1}{2} \\&=\|\nabla u \|_{L^2}\end{aligned} \]
が導入できます。この簡略化されたノルムを、標準的な\(H^1\)ノルムに対し、\(H_0^1\)ノルムと呼びましょう。
ポアンカレの不等式は、\(\|u\|_{L^2} \leq C \|u\|_{H_0 ^1}\)と表せます。
ポアンカレの不等式を用いれば、\(H^1\)ノルムと\(H_0^1\)ノルムが、ノルムとして同値であることが示せます。
\[\begin{aligned} & \|u\|_{H_0 ^1} ^2 \\ &\leq \|u\|_{H^1}^2 \\&= \|u\|_{L^2}^2 +\|u\|_{H_0^1}^2 \\ &\leq C\|\nabla u\|_{L^2}^2+\|u\|_{H_0^1}^2\\ &=(C+1) \|u\|_{H_0 ^1}^2 \end{aligned}\]
となるので。
\(H_0 ^1\)ノルムに対応する内積として、
\[\langle u,v\rangle :=\sum_{ |\alpha| = 1} \langle D^{\alpha} u, D^{\alpha} v\rangle_{L^2}\]
も利用できます。
以上、ポアンカレの不等式とは、証明、\(H_0^1\)ノルムへの応用を紹介してきました。
\(H_0 ^1\)の関数のノルムは、その勾配(1階微分)のノルムでおさえられるので、不等式評価が簡単になります。これは反応拡散方程式のアトラクターの存在を示すためにも、基本的なものとなるでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
Evans, Lawrence C.(著)
¥16,299 (2022-08-19時点)