複素解析における最大値の原理とは：例、注意点

どうも、木村（@kimu3_slime）です。

今回は、複素解析における最大値の原理とは何か、例や注意点を紹介します。

最大値の原理（maximum principle）

\(U\)を\(\mathbb{C}\)の領域（連結な開集合）とし、\(f\)を\(U\)上の正則関数で、定数関数でないとする。このとき、\(f\)は\(U\)上で最大値を持たない。

さらに、閉包\(\mathrm{Cl}(U)\)が有界（コンパクト）で、\(f\)が境界\(\partial U\)込みで連続とする。\(f\)の定義域を\(\mathrm{Cl}(U)\)とするとき、\(f\)は境界\(\partial U\)において最大値を持つ。

\[ \begin{aligned}\max _{z \in \mathrm{Cl}(U) }|f(z)|=\max _{z \in \partial U }|f(z)|\end{aligned} \]

この主張が何を言っているのか、例を通じて考えてみましょう。

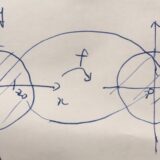
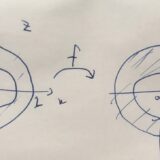
\(f(z)=z\)、\(U=\{z \mid |z|<1\}\)とします。極形式\(z=re^{i\theta}\)で表示すれば、その大きさは\(|f(z)|=r\)です。これは\(U\)上では最大値を持ちません。例えば\(z= \frac{9}{10}\)のとき\(|f(z)|=\frac{9}{10}\)ですが、\(\frac{9}{10}+\frac{1}{20}\)という点を考えればより大きな値を持ちません。円盤内のどんな点を考えても、\(|z|=1\)側により高い値を持つ点があるのです。

この例では、閉包は\(\mathrm{Cl}(U)=\{z \mid |z|\leq 1\}\)で、境界は\(\mathrm{Cl}(U)=\{z \mid |z|= 1\}\)です。そして、境界上のすべての点\(z\)で、最大値\(|f(z)|=1\)を取ります。実際、境界上の点ならば値は等しく、内部の点\(w\)と比較すると\(r =|f(w)|<|f(z)|=1 \)となっているので。このような状況を一般化するのが、最大値の原理です。

「定数関数でない」という仮定ですが、定数関数を考えれば境界上でも同じ値を取り、内部でも最大値を取ることになります。例えば\(f(z)=0\)で同じ領域を考えれば、\(z=0\)でも\(|z|=1\)でも同じ値を取り、すべての\(z\in \mathbb{C}\)で最大値を取っています。

また、最大値の存在に関する主張で、閉包が有界という仮定は必要であることに注意しましょう。例えば、第一象限\(U=\{z \mid x,y \geq 0\}\)を考えると、境界は実軸、虚軸の正の部分です。\(f(z)=z\)を考えると、実軸上で\(f(x)=x\)なので、限りなく大きな値を持ち、最大値を持ちません。有界な閉集合の連続関数でなければ、最大値を持つとは限らないわけです。

参考：コンパクト性とは：有界閉集合、最大値の定理を例に

ちなみに、単なる実関数については、類似の主張は成り立ちません。例えば\(f(x)=x(x-1)\)、\(U=(0,1)\)とすると、\(|f(x)|\)は内部\(x= \frac{1}{2}\)で最大値を持ちます。

最大値の原理は、平均値の性質や開写像定理から示せることが知られています。証明については、神保「複素関数入門」やエリアス・ラミ「複素解析」を参照してください。

今回紹介したのは複素解析における最大値の原理ですが、同様の性質が、実調和関数（ラプラス方程式）の解についても成り立ちます。すなわち、調和関数は考えている有界領域の内部で最大値を取らず、境界で最大値を取るわけです。

最大値の原理は、ラプラス方程式のディリクレ境界値問題の解の一意性を保証してくれるもので、調和関数の基本的な性質のひとつ、と言えます。

以上、複素解析における最大値の原理とは何か、例や注意点を紹介してきました。

例えば、線形分数変換の大きさが一定の値以下であることを示すために、最大値の原理は使えます。リウビルの定理などと合わせ、正則関数の基本的な性質として知っておくと良いでしょう。

木村すらいむ（@kimu3_slime）でした。ではでは。