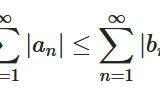収束する数列は有界であることの証明と応用

どうも、木村（@kimu3_slime）です。

今回は、収束する数列は有界であることの証明と応用を紹介します。

示したい主張は、次の通り。

\((a_n)_{n=0}^\infty\)を収束する数列とし、極限を\(\lim_{n\to \infty} a_n =\alpha\)としましょう。このとき、この数列は有界であること、つまり「すべての\(n \geq 0\)に対し、\(|a_n|\leq M\)」を満たす\(M\)が存在します。

収束の定義\(\lim_{n\to \infty} a_n =\alpha\) は、任意の\(\varepsilon >0\)に対し、「\(n \geq N\)ならば\(|a_n – \alpha|<\varepsilon\)」を満たすような\(N \in \mathbb{N}\)が存在することでした。

ここで例えば\(\varepsilon=1\)とすると、「\(n \geq N\)ならば\(|a_n – \alpha|<1\)」を満たす\(N \in \mathbb{N}\)が存在します。つまり、十分先の番号では、数列と\(\alpha\)の差の大きさは1以下に抑えられているわけです。特に、\(n \geq N\)のときは、三角不等式

\[ \begin{aligned} |a_n| &= |(a_n-\alpha)+\alpha|\\&< |a_n- \alpha|+|\alpha|\\ &<1+|\alpha|\end{aligned} \]

から、\(M_1:= 1+|\alpha|\)と置くことで、

\[ \begin{aligned}|a_n| < M_1\end{aligned} \]

が成り立ちます。そして、\(M_2 :=\max \{|a_0|,\dots,|a_{N-1}|\}\)としましょう。\(N\)より前の項は有限個なので、それらの大きさを最大値を考えます。

以上をまとめて、\(M:=\max\{M_1,M_2\}\)とおけば、すべての\(n\in \mathbb{N}\)に対し、\(|a_n| \leq M\)が成り立ちます。\(n\)が小さいケースでは\(M_2\)で、大きいケースでは\(M_1\)で抑えられているわけです。よって、\((a_n)\)が有界であることが示せました。

この主張は、さまざまなところで利用されます。例えば、収束する級数の各項は0へ収束することと合わせて、

\[ \begin{aligned}|a_k (z_1-z_0)^k| < M\end{aligned} \]

といった評価をするために使えます。

参考：べき級数の収束発散が円盤によって分かれること：収束半径の性質

収束する数列は有界でなければなりませんが、その逆は一般には成り立ちません。

つまり、有界な数列は収束する数列とは限りません。例としては\(a_n=(-1)^n\)があります。\(|a_n| \leq 1\)で有界ですが、収束しません。

ただし、条件がつけば収束します。例えば、有界な単調数列は収束します。より一般には、有界な数列は収束する部分列を持ちます（ボルツァーノ・ワイエルシュトラスの定理）。

参考：数列と上限・下限の関係：有界な単調数列は収束する、部分列、ボルツァーノ・ワイエルシュトラスの定理とは：点列コンパクトとの関係

以上、収束する数列は有界であることの証明と応用を紹介してきました。

収束・有界の定義やイメージを知っていれば、確かに有界でありそうなものですが、それをきちんと定義にもとづいて示せるのは大事なことです。

慣れれば当たり前に思える簡単な議論なので、ぜひ習得してみてください。

木村すらいむ（@kimu3_slime）でした。ではでは。