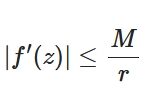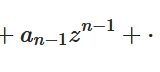複素関数のテイラー展開（べき級数展開）とは、証明

どうも、木村（@kimu3_slime）です。

今回は、複素関数のテイラー展開（べき級数展開）とは何か、その証明を紹介します。

実数値関数は、無限回微分可能で、かつ剰余項が消える\(\lim _{n\to \infty}R_{n+1}(x) =0\)ならば、

\[ \begin{aligned}f(x) = \sum_{k=0}^\infty \frac{f^{(k)}(a)}{k!}(x-a)^k\end{aligned} \]

というべき級数として展開できる（テイラー展開）のでした。

複素微分可能な関数、正則関数でも、同じように必ずテイラー展開することができます。

\(D\)を\(z_0\)を中心とする半径\(r\)の円盤とし、\(f\)をそこで正則な関数としましょう。このとき、\(f\)は\(z_0\)を中心としてテイラー展開可能、すなわち

\[ \begin{aligned}f(z)= \sum_{n=0}^\infty a_n (z-z_0)^n\end{aligned} \]

\[ \begin{aligned} a_n &= \frac{f^{(n)}(z_0)}{n!} \end{aligned} \]

と表すことができます。つまり、この級数は円盤\(D\)上で収束します。

特に、\(f\)が複素数\(\mathbb{C}\)全体で正則なときは、テイラー展開はすべての点に対して成り立つことになります。例えば、指数関数

\[ \begin{aligned}e^{z} =\sum_{n=0}^\infty \frac{1}{n!}z^n \end{aligned} \]

や三角関数といった初等関数のテイラー展開は、実数の場合と全く同じように成り立ちます（そもそも、これらのべき級数展開を定義式とすることもありますが）。

テイラー展開の形は複素と実で全く同じですが、その展開可能性の条件は異なっています。

正則関数は、1回複素微分可能と仮定するだけで、必ず無限回微分可能かつテイラー展開可能（解析的）になります。実数関数は、無限回微分可能であるからといって、テイラー展開できるとは限りません（剰余項が消えなければならない）。つまり、正則性は実微分可能性より強い仮定というわけです。

では、正則関数のテイラー展開が可能あることを証明しましょう。

出発点とするのは、コーシーの積分公式とその応用

\[ \begin{aligned}f(z) =\frac{1}{2\pi i}\int_c \frac{f(w)}{w-z}dw\end{aligned} \]

\[ \begin{aligned}f^{(n)}(z) = \frac{n!}{2\pi i} \int_c \frac{f(w)}{(w-z)^{n+1}}dw\end{aligned} \]

です。ここで\(c\)は考えている円盤の円周で、\(f\)は円盤上で正則なので、コーシーの積分公式が使えます（円盤は単連結な領域）。

これをべき級数展開の形に変えるため、被積分関数を級数展開しましょう。

\[ \begin{aligned} &\frac{1}{w-z}\\&= \frac{1}{(w-z_0)-(z-z_0)}\\ &=\frac{1}{w-z_0} \frac{1}{1-\frac{z-z_0}{w-z_0}}\end{aligned} \]

と変形できます。ここで\(z\)は円盤内の点なので、\(R\)を\(R< r\)を満たす数として\(|z-z_0| \leq R\)です。また、\(w\)は円周上の点なので、\(|w-z_0|=r\)です。したがって、

\[ \begin{aligned}|\frac{z-z_0}{w-z_0}|< \frac{r}{r}=1 \end{aligned} \]

となります。つまり、公比を\(|\frac{z-z_0}{w-z_0}|\)と見ることで、等比級数の和の公式から

\[ \begin{aligned}\frac{1}{1-\frac{z-z_0}{w-z_0}}= \sum_{n=0}^\infty( \frac{z-z_0}{w-z_0})^n\end{aligned} \]

と展開できます。この級数は\(w\)について一様収束していることが示せて（詳しくは神保「複素関数入門」など参照）、したがって項別微分が可能になります。この結果を利用すれば、

\[ \begin{aligned} f(z) &=\frac{1}{2\pi i}\int_c \frac{f(w)}{w-z}dw\\ &=\frac{1}{2\pi i}\int_c f(w) \sum_{n=0}^\infty \frac{(z-z_0)^n}{(w-z_0)^{n+1}} dw \\ &=\frac{1}{2\pi i} \sum_{n=0}^\infty (\int_c \frac{f(w)}{(w-z_0)^{n+1}}dw ) (z-z_0)^n \end{aligned} \]

とべき級数展開できました。ここで積分公式

\[ \begin{aligned}f^{(n)}(z) = \frac{n!}{2\pi i} \int_c \frac{f(w)}{(w-z)^{n+1}}dw\end{aligned} \]

と係数を比較すると、それは

\[ \begin{aligned} a_n&=\frac{1}{2\pi i} \int_c \frac{f(w)}{(w-z_0)^{n+1}}dw \\ &= \frac{f^{(n)}(z)}{n!}\end{aligned} \]

であることがわかります。

まとめると、コーシーの積分公式と等比級数の展開から、べき級数展開が導かれるという流れです。

以上、複素関数のテイラー展開（べき級数展開）とは何か、その証明を紹介してきました。

コーシーの積分定理は、正則関数やその導関数の「一点」での値を、「周囲での」値（周回積分）として表すことができ、そこからテイラー展開可能性すら導ける強力な結果です。

正則関数がべき級数展開できることは当たり前の結果として利用されがちですが、その発想を支えているのがコーシーの積分定理と知っておくと良いでしょう。

木村すらいむ（@kimu3_slime）でした。ではでは。