2次元長方形領域でのラプラス方程式の解き方

どうも、木村（@kimu3_slime）です。

今回は、2次元長方形領域でのラプラス方程式の解き方を紹介します。

考えるのは、

\[ \begin{aligned}\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}=0\end{aligned} \]

というラプラス方程式です。考える領域は\(R:=[0,a]\times[0,b]\)という長方形で、境界条件としては、

\[ \begin{aligned}u(x,0)= 0 \\ u(0,y)=0 \\ u(a,y)=0\\u(x,b)=g(x)\end{aligned} \]

というディリクレ境界条件を考えることにします。上側の辺での値が\(g(x)\)で、他は0です。

この方程式は、変数分離法とフーリエ級数によって解くことができます。

まず、\(u(x,y)=F(x)G(y)\)と表される変数分離形の解を探しましょう。

例えば\(\frac{\partial^2 u}{\partial x^2}= \frac{d^2 F}{d x^2}G\)となるので、それを方程式に代入すると、

\[ \begin{aligned}\frac{d^2 F}{d x^2}G +F\frac{d^2 G}{d y^2}=0\end{aligned} \]

です。自明な解\(u \equiv 0\)以外を考えると、\(F,G \neq 0\)となる点が存在します。そこで両辺を\(FG\)で割って整理すると

\[ \begin{aligned}\frac{1}{F}\frac{d^2 F}{d x^2} =-\frac{1}{G}\frac{d^2 G}{d y^2}\end{aligned} \]

となります。左辺は\(x\)のみ、右辺は\(y\)のみに依存するので、両辺は\(x,y\)に依存しない定数（分離定数）です。そこで両辺を\(-\lambda \)と置くと、

\[ \begin{aligned}\frac{d^2 F}{d x^2} = -\lambda F\end{aligned} \]

\[ \begin{aligned}\frac{d^2 G}{d y^2} = \lambda G\end{aligned} \]

という2つの常微分方程式が得られました。

参考：同次形の2階線形微分方程式の解き方、学ぶ意味：熱方程式への応用を例に

まず、\(F\)の方程式の一般解は、

\[ \begin{aligned}F(x)= C_1 \cos \sqrt{\lambda} x +C_2 \sin \sqrt{\lambda} x\end{aligned} \]

です。境界条件\(u(0,y)=0 , u(a,y)=0\)から、\(F(0)=0,F(a)=0\)となります。すると、\(C_1 =0\)で、\(C_2 \)は任意です。非自明な解を考える、すなわち\(C_2 \neq 0\)のときを考えると、

\[ \begin{aligned}\sin \sqrt{\lambda} a =0\end{aligned} \]

です。これを\(\lambda \)について解けば、\(\sqrt{\lambda} a=n\pi\)、\(\lambda = (\frac{n\pi}{a})^2\)、\(n\)は整数です。

\[ \begin{aligned}F_n (x) = \sin \frac{n\pi x}{a}\end{aligned} \]

は解です。

この\(\lambda\)を使って、\(G\)に関する方程式も解きましょう。すると、

\[ \begin{aligned}G_n(y)=A_n e^{\sqrt{\lambda} y} +B_n e^{-\sqrt{\lambda} y} \\ =A_n e^{\frac{n \pi y}{a} } +B_n e^{-\frac{n \pi y}{a}} \end{aligned} \]

となります。境界条件\(u(x,0)= 0\)から、\(G_n(0)=0\)です。したがって、\(A_n+B_n=0\)となります。これを使って整理すれば、

\[ \begin{aligned}G_n(y)=A_n e^{\frac{n \pi y}{a} } -A_n e^{-\frac{n \pi y}{a}} \\ =2 A_n \sinh \frac{n \pi y}{a}\end{aligned} \]

となりました。

参考：双曲線関数をなぜ学ぶか？懸垂線、微分と積分の性質

よって、

\[ \begin{aligned}u_n (x,y) =F_n(x)G_n(y)\\ =2A_n \sin \frac{n\pi x}{a} \sinh \frac{n \pi y}{a}\end{aligned} \]

は、3つの境界条件を満たす解とわかりました。

残すは、\(u(x,b)=g(x)\)を満たす解を構成することです。これを\(u_n\)の級数として

\[ \begin{aligned}u(x,y) = \sum_{n=1}^\infty u_n(x,y)\end{aligned} \]

という形で構成しましょう。

関数\(g\)は、境界条件\(g(0)=g(a)=0\)から、フーリエ級数

\[ \begin{aligned}g(x) = \sum_{n=1}^\infty b_n \sin \frac{n\pi x}{a}\end{aligned} \]

\[ \begin{aligned}b_n =\frac{2}{a} \int_0^a g(x) \sin \frac{n\pi x}{a} dx \end{aligned} \]

として展開できます。

ここで、\(u(x,b)=g(x)\)の式より

\[ \begin{aligned}\sum_{n=1}^\infty (2A_n \sinh \frac{n \pi b}{a} )\sin \frac{n\pi x}{a} \\ \sum_{n=1}^\infty b_n \sin \frac{n\pi x}{a} \end{aligned} \]

となっています。同じ形ができたので、係数\(A_n\)を決定することができます。

\[ \begin{aligned}A_n = \frac{b_n}{2 \sinh \frac{n \pi b}{a}} \\ =\frac{1}{a \sinh \frac{n \pi b}{a}} \int_0^a g(x) \sin \frac{n\pi x}{a} dx \end{aligned} \]

よって、

\[ \begin{aligned}u(x,y) = \sum_{n=1}^\infty 2A_n \sin \frac{n\pi x}{a} \sinh \frac{n \pi y}{a}\end{aligned} \]

がすべての境界条件を満たすことがわかりました。

厳密に言えば、級数が収束し、微分可能であることを示す必要がありますが、ここでは省略します。

参考：関数項級数の一様収束、Mテストとは：熱方程式への応用

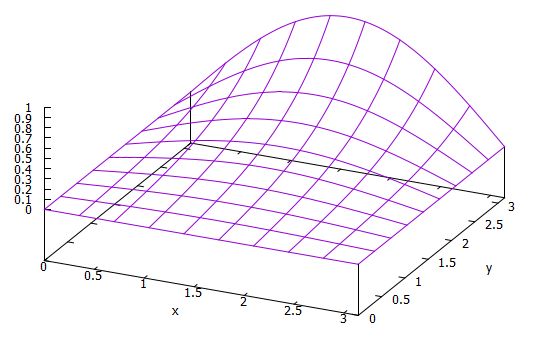
ラプラス方程式の解を、具体的にひとつ得てみましょう。

\(a=b=\pi\)、\(g(x)= \sin x\)とします。係数は\(n=1\)のときは

\[ \begin{aligned}A_1 = \frac{1}{\pi \sinh \pi} \int_0^\pi ( \sin x)^2 dx \\= \frac{1}{2 \sinh \pi}\end{aligned} \]

です。\(n \geq 2\)のときは、三角関数の直交性から\(A_n =0\)です。よって、

\[ \begin{aligned}u(x,y)= \frac{1}{ \sinh \pi} \sin x \sinh y\end{aligned} \]

となりました。確かにこれはラプラス方程式を満たし（\(\sin\)は2回微分で符号変化し、\(\sinh\)は2回微分で符号変化しない）、境界条件もすべて満たしています。