どうも、木村(@kimu3_slime)です。
今回は、2次元線形力学系の平衡点の分類:サドル(鞍点)とは何か紹介します。
2次元の線形力学系とは
2次元(平面)の線形力学系とは、\(x(t)=(x_1(t),x_2(t))\)、\(A\)をサイズ\(2,2\)の行列として
\[ \begin{aligned}\frac{dx}{dt}= Ax\end{aligned} \]
と表される連立常微分方程式のことです。
\(Ax=0\)を満たす解、つまり\(x=0\)を平衡解(定常解、固定点、臨界点)と呼びます。
参考:方程式を解かずに、解の軌跡・安定性を調べてみよう 力学系理論入門、線形微分方程式の解の安定性は「固有値」を調べればわかる、1次元の線形力学系とは:相図の書き方、安定性
2次元の力学系では、平衡解はおよそ3つに分類されます。
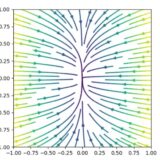
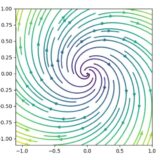
- ノード(結節点)
- サドル(鞍点)
- スパイラル(渦状点)
今回はサドルについて紹介しましょう。
解の挙動は、行列の固有値によって影響を受けます。行列の成分を
\[ \begin{aligned}A= \begin{pmatrix} a&b\\ c&d \end{pmatrix}\end{aligned} \]
と表すとき、その固有方程式は
\[ \begin{aligned} &\det (\lambda I-A) \\&= \lambda^2 -(a+d)\lambda +(ad-bc)\\ &= \lambda^2 -\mathrm{tr}A \lambda +\det A\\&= 0 \end{aligned} \]
となるので、固有値は
\[ \begin{aligned} \lambda = \frac{\mathrm{tr} A \pm \sqrt{(\mathrm{tr} A) ^2 – 4 \det A}}{2} \end{aligned} \]
となります。
サドルとは
2つの固有値がともに実数で、異なる符号であるとき、平衡解はサドル(鞍点 saddle)であると呼ばれます。
つまり、\((\mathrm{tr} A) ^2 – 4 \det A\geq 0\)、\(\det A = \lambda_1 \lambda_2 < 0\)のケースです。
\[ \begin{aligned}A= \begin{pmatrix} 1&0\\ 0&-2 \end{pmatrix}\end{aligned} \]
のとき、固有値は\(1,-2\)で、対応する固有ベクトルは\((1,0),(0,1)\)です。
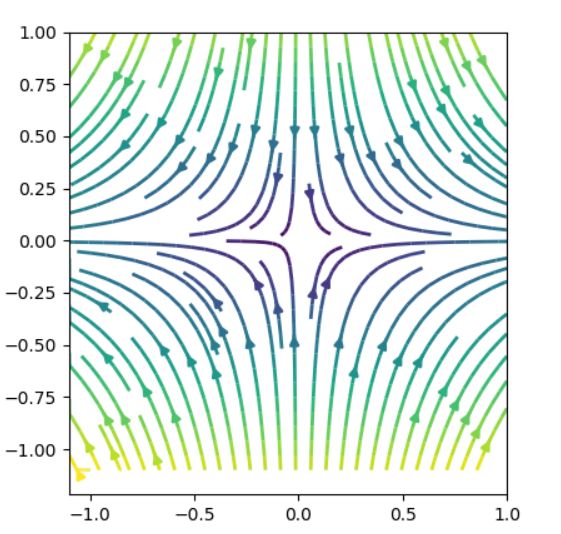
解は一般に\(x(t) =(C_1 e^t,C_2 e^{-2t} )\)と表されます。ここから\(t\)を消去すると、\( x_2 = \frac{C_1^2 }{C_2}\frac{1} {x_1 ^2}\)という曲線が得られますね。
サドル(馬に座るための椅子)という名前は、サドル面のように、原点付近で上がっていく方向と下がっていく方向、解が近づいていく方向と離れていく方向の両方があるようすを表しているのでしょう。
実部が正の固有ベクトル\((1,0)\)の方向を考えると、\(x(t)=(C_1e^{t},0)\)となって原点から離れていくので、平衡解は不安定です。ノードは安定なケースと不安定なケースがありましたが、サドルは必ず不安定になります。
ノードでは、固有値が重複して退化するケースがありました。しかし、サドルはそもそも実部が異符号な固有値を考えているので、退化することはありえません。
応用としては、サドルは、振り子の運動方程式を\(x= (\pi,0)\)において線形化した方程式として表れます。振り子で言えば真上の初期状態がサドルに対応し、それは不安定な状態です。
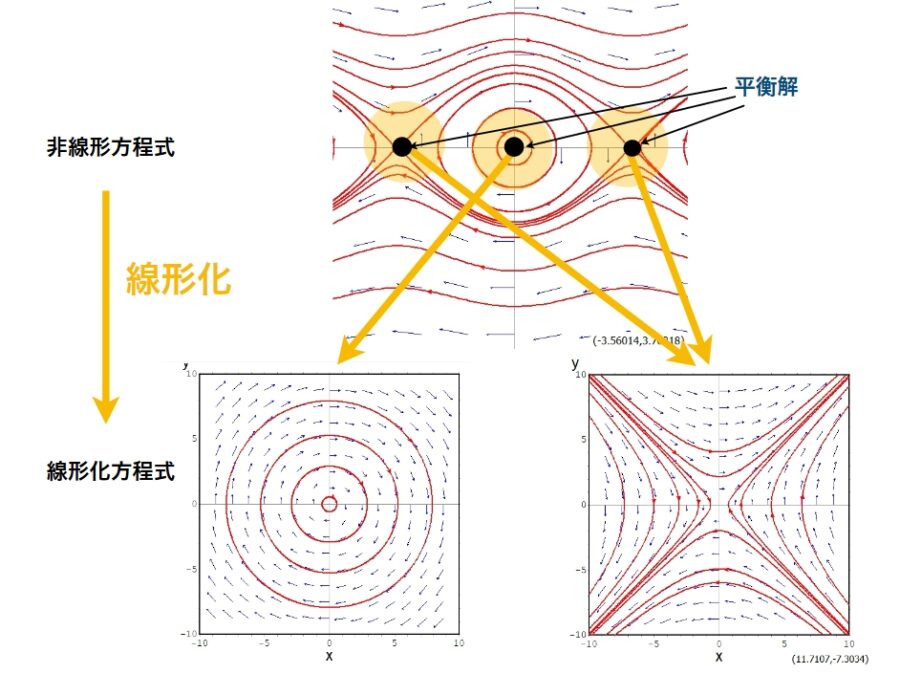
固有ベクトル上の解は、時間経過してもそこから外れることはありません。これらは安定空間、不安定空間と呼ばれるものです。
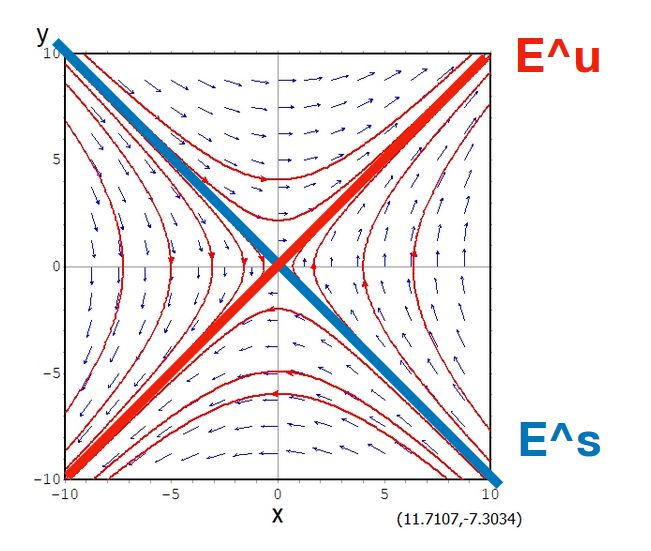
以上、2次元線形力学系の平衡解の分類として、サドルについて簡単な例を交えて紹介してきました。
2つの固有ベクトルがあって、一方は平衡解に近づき、もう一方は平衡解から離れる。そうした不安定な平衡解がサドルというわけでした。
木村すらいむ(@kimu3_slime)でした。ではでは。
Pearson (2016-03-02T00:00:00.000Z)
¥4,910
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥6,333 (中古品)
朝倉書店 (2002-01-01T00:00:01Z)
¥2,215 (中古品)
こちらもおすすめ
方程式を解かずに、解の軌跡・安定性を調べてみよう 力学系理論入門
なぜ行列式を学ぶのか? 固有値・固有ベクトルの求め方:固有多項式の定義