どうも、木村(@kimu3_slime)です。
今回は、全微分とはなにか、定義、十分条件、全微分可能でない例を紹介します。
前提知識:2変数関数と偏微分:グラフ、接平面を描いてみよう、方向微分、法線微分の定義、例、求め方
全微分とは
簡単なケースとして、2変数関数\(f:\mathbb{R}^2 \to \mathbb{R}\)のについて考えましょう。\(f(x,y)= x^2+y^2\)のように、2変数の関数のグラフは、一般に曲面になっています。
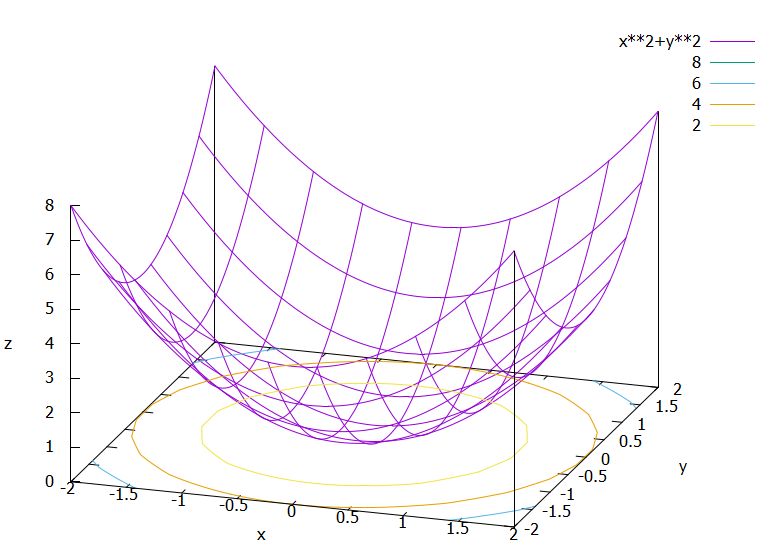
1変数関数で、グラフの接線を求める操作として微分を定義したように、2変数ならばグラフの接平面を求める操作は定義できないでしょうか。それが全微分です。
1変数関数の微分の定義は
\[ \begin{aligned}\lim_{h \to 0} \frac{f(x+h)-f(x)}{h}= c\end{aligned} \]
でしたが、これを
\[ \begin{aligned}\lim_{h \to 0} \frac{f(x+h)-f(x) -ch}{h}=0 \end{aligned} \]
と変形することで一般化します。
多変数の問題では、\(x=(x_1,x_2)\)、\(h= (h_1,h_2)\)と変数がベクトルになります。それに応じて、微分係数も\(c=(c_1,c_2)\)とベクトルになります。
\[ \begin{aligned}\lim_{h \to 0}\frac{f(x+h)-f(x)-\langle c,h\rangle}{\|h\|}=0\end{aligned} \]
を満たす\(c=(c_1,c_2)\)が存在するとき、\(f\)は全微分可能(totally differentiable)であるといい、\(f^\prime (x)=c\)と表します。\(\langle c,h\rangle=c_1h_1+c_2h_2\)はベクトルの内積、\(\|h\|= \sqrt{h_1^2+h_2^2}\)はノルム(大きさ)です。全微分可能のことを、単に微分可能と呼ぶことがあります。
例えば、\(f(x,y)=x^2+y^2\)は各点で全微分可能で、導関数は\(c=f^\prime(x,y)= (2x,2y)\)です。確かめてみましょう。
\[ \begin{aligned}f(x+h_1,y+h_2)=(x+h_1)^2+(y+h_2)^2 \\=x^2+y^2+2xh_1+2yh_2+h_1^2+h_2^2\end{aligned} \]
\[ \begin{aligned}\langle c,h\rangle=2xh_1+2yh_2\end{aligned} \]
なので、分子ではうまくキャンセルが起こっていて、
\[ \begin{aligned} & \frac{\|f(x+h)-f(x)-\langle c,h\rangle\|}{\|h\|} \\&= \frac{h_1^2+h_2^2}{\sqrt{h_1^2+h_2^2}}\\&= \sqrt{h_1^2+h_2^2}\end{aligned} \]
となり、\(h \to 0\)で0に収束します。
導関数、全微分係数\(f^\prime(x,y)= (2x,2y)\)は、接平面の傾きに対応するものです。例えば、\((x,y)=(1,1)\)における接平面の方程式は\(g(x,y)=2(x-1)+2(y-1)+2\)です。
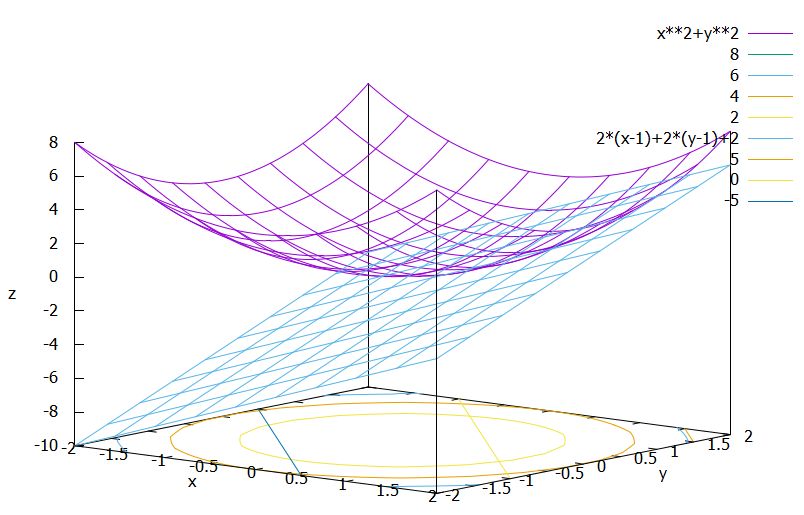
全微分の定義
\[ \begin{aligned}\lim_{h \to 0}\frac{\|f(x+h)-f(x)-\langle f^{\prime}(x),h\rangle\|}{\|h\|}=0\end{aligned} \]
は、次のように解釈できます。\(f(x+h)-f(x)\)は、\(f\)の値の変化です。\(\langle f^{\prime}(x), h\rangle\)は、\(h_1,h_2\)の1次式であり、\(f^{\prime}(x)\)を係数とする平面の方程式です。
つまり、関数\(f\)は平面\(\langle f^{\prime}(x), h\rangle\)で近似できる、といっているわけですね。分母\(\|h\|\)を取ることは、1次式(線形的)な近似であり、2次以上の変化を無視していることを表しています。
多変数関数、ベクトル値関数(ベクトル場)についても、全微分は同様に定義されます。
\[ \begin{aligned}\lim_{h \to 0} \frac{f(x+h)-f(x) -ch}{\|h\|}=0 \end{aligned} \]
\[ \begin{aligned}\lim_{h \to 0} \frac{\|f(x+h)-f(x) -Ch\|}{\|h\|}=0 \end{aligned} \]
\(f: \mathbb{R}^N \to \mathbb{R}\)ならば、微分係数\(c\)は\(N\)次元のベクトルです。\(f:\mathbb{R}^N \to \mathbb{R}^M\)ならば、微分係数\(C\)は\((M,N)\)行列となります。
といってもイメージしづらいと思うので、全微分可能性の十分条件を知ると良いでしょう。
全微分の十分条件
\(f\)が各成分について偏微分可能であり、偏導関数が連続である(\(C^1\)級という)ならば、\(f\)は全微分可能であることが知られています。
このとき、\(f: \mathbb{R}^N \to \mathbb{R}\)ならば、微分係数は
\[ \begin{aligned}f^\prime (x)=\nabla f:=\mathrm{grad} f:\\=(\frac{\partial f}{\partial x_1},\dots,\frac{\partial f}{\partial x_N})\end{aligned} \]
と各偏導関数を並べたベクトル(勾配ベクトル)によって計算できます。
この方法はとても簡単です。例えば、\(f(x,y)=x^2-y^2\)について考えてみましょう。偏導関数を計算すると、\(\frac{\partial f}{\partial x}=2x\)、\(\frac{\partial f}{\partial y}= -2y\)で、これらは連続です。したがって、全微分可能であり、全微分係数は\(f^{\prime}(x,y)=(2x,-2y)\)と言えます。
ベクトル場\(f: \mathbb{R}^N \to \mathbb{R}^M\)、\(f(x)=(f_1(x),\dots,f_M(x))\)については、全微分係数は
\[ \begin{aligned} f^\prime(x)&= J_f(x)\\&:= \begin{pmatrix} \frac{\partial f_1}{\partial x_1}(x) &\dots &\frac{\partial f_1}{\partial x_N}(x) \\ \vdots &\vdots\\\frac{\partial f_M}{\partial x_1}(x) &\cdots &\frac{\partial f_M}{\partial x_N}(x) \end{pmatrix} \end{aligned} \]
という行列になり、これを\(f\)のヤコビ行列(Jacobi matrix)と言います。
例えば、\(N=M=2\)、\(F(x,y)=(y,-\sin x)\)ならば、その全微分係数は
\[ \begin{aligned}J_F(x,y)=\begin{pmatrix} 0&1\\ -\cos x &0\end{pmatrix}\end{aligned} \]
です。
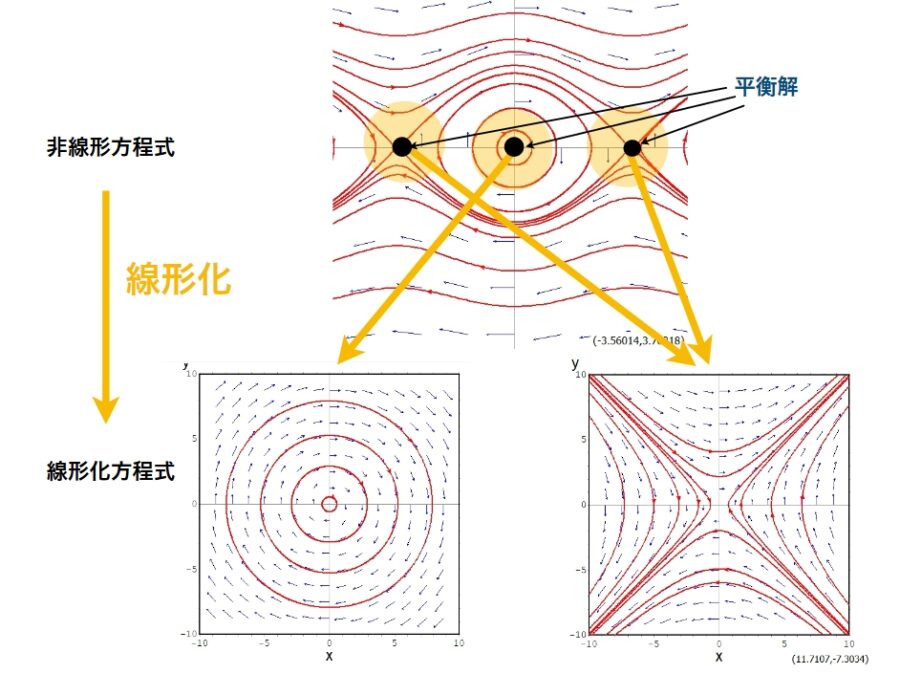
参考:ベクトル値関数をベクトル場として描いてみよう:ヤコビ行列と線形近似、微分方程式の安定性を調べる「線形化」の方法とは?
偏微分可能だが全微分可能でない例
一般論として、全微分可能であるならば、各変数について偏微分可能であることが知られています。
さきほどは、「各変数について偏微分可能であり、かつ偏導関数が連続ならば全微分可能」という主張を紹介しました。
つまり、偏導関数が存在することは、全微分可能にとって十分ではないのです。
実際、すべての方向について方向微分可能であるのに、全微分可能でない例を紹介しましょう。
\[ \begin{aligned}f(x,y)= \begin{cases}\frac{x|y|}{\sqrt{x^2+y^2}} & ((x,y)\neq 0)\\0 & ((x,y)=0)\end{cases}\end{aligned} \]
原点以外では、全微分可能です。原点でのようすに注目します。
\((a,b) \neq 0\)を任意のベクトルとして、原点では\((a,b)\)方向に方向微分可能であることを確かめます。
\[ \begin{aligned} &\lim_{h\to 0} \frac{f(0+h(a,b)-f(0))}{h} \\&=\lim_{h\to 0} \frac{\frac{ha|hb|}{\sqrt{h^2 a^2+h^2b^2}}}{h} \\&= \frac{a|b|}{\sqrt{a^2+b^2}}\end{aligned} \]
となるので、方向微分可能です。
しかし、全微分可能ではありません。
背理法として、全微分可能で、微分係数は\(c=(c_1,c_2)\)としましょう。\(h=(h_1,h_2)\)と表すとき、\(h_2= kh_1\)、\(h_1,k>0\)となる近づき方を考えます。すると、
\[ \begin{aligned} &\frac{\|f(h)-f(0)-\langle c,h\rangle\|}{\|h\|}\\&=\frac{\frac{h_1|kh_1|}{\sqrt{h_1^2+k^2h_1^2}}-c_1h_1-c_2kh_1}{\sqrt{h_1^2+k^2h_1^2}}\\&= \frac{kh_1^2-h_1^2\sqrt{1+k^2}(c_1+kc_2)}{h_1^2(1+k^2)} \\ &= \frac{k-\sqrt{1+k^2}(c_1+kc_2)}{1+k^2}\end{aligned} \]
となるので、\(h\to 0\)の極限を取れば、全微分可能であることから、
\[ \begin{aligned}\frac{k-\sqrt{1+k^2}(c_1+kc_2)}{1+k^2}=0\end{aligned} \]
です。特に\(k=1,2,3\)のときの分子を考えると、
\[ \begin{aligned}1 =\sqrt{2}(c_1+c_2)\end{aligned} \]
\[ \begin{aligned}2 =\sqrt{5}(c_1+2c_2)\end{aligned} \]
\[ \begin{aligned}3 =\sqrt{10}(c_1+3c_2)\end{aligned} \]
といった式が成り立ちますが、これを\(c_1,c_2\)に関する連立方程式と見たとき、変数の数より方程式の本数が多いため、解は存在しません。これは全微分可能という仮定に反し、矛盾です。よって、全微分不可能と言えます。
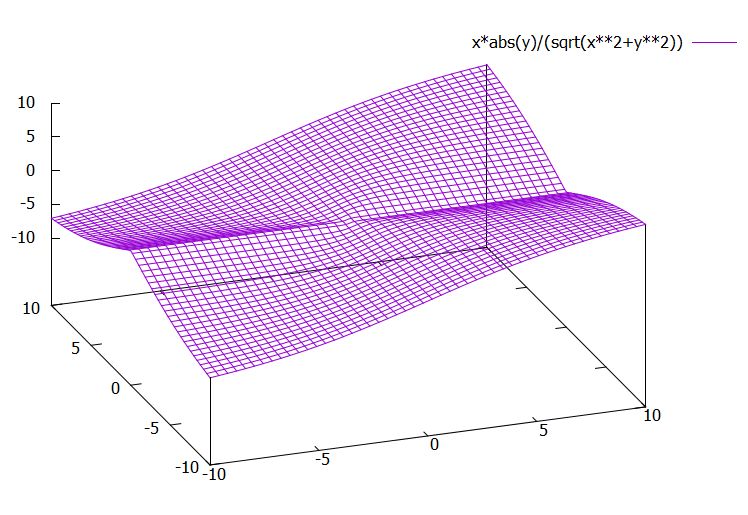
原点にどんな方向から近づいても、その方向から見たグラフの傾き(方向微分)自体は定まっています。しかし、原点に接するようなひとつの接平面は作れそうにありません。1変数では\(f(x)=|x|\)が微分可能でないように、\(|y|\)の部分によって「接平面」の可能性が2つ以上生まれてしまっています。
以上、全微分とはなにか、定義、十分条件と求め方、全微分可能でない例を紹介してきました。
全微分可能とは「接平面が存在する」ということで、「接線が存在する」という1変数の微分の素直な拡張となっています。
しかし多変数の場合は、紹介した例のように、全微分可能と偏微分可能が別物になるケースがあります。
その面倒臭さを避けるための簡単な仮定として、「各成分について偏微分可能であり、偏導関数が連続である(連続微分可能:\(C^1\)級)」は便利です。この条件があるときは、極限の議論をしなくても、偏導関数を使って簡単に全微分を求められるでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
共立出版 (1984-12-21T00:00:01Z)
¥682 (中古品)
岩波書店 (1978-03-23T00:00:01Z)
¥5,060
岩波書店 (1981-11-15T00:00:01Z)
¥5,720
東京大学出版会 (1980-03-31T00:00:01Z)
¥3,080
東京大学出版会 (1985-04-25T00:00:01Z)
¥1,884 (中古品)
こちらもおすすめ
ベクトル値関数をベクトル場として描いてみよう:ヤコビ行列と線形近似






