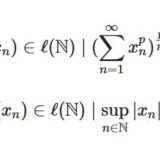部分空間とは：例、判定法、証明の書き方

どうも、木村（@kimu3_slime）です。

今回は、線形代数学における部分空間とは何か、その例と証明の書き方を紹介します。

線形空間の入門：実数空間、線形結合、線形部分空間、次元とは何か：2次元を例に

部分空間とは
部分空間の例と証明
こちらもおすすめ

部分空間とは

まず、定義を確認しておきましょう。

部分空間とは、線形空間の部分集合であって、かつ線形空間であるものです。

\(V\)を線形空間（ベクトル空間）とします。\(W\)が\(V\)の部分空間（subspace）であるとは、

\(W\)が\(V\)の部分集合である \(W \subset V\)
\(V\)の演算について、\(W\)が閉じている
1. 和について閉じている：\(x,y \in W\)ならば、\(x+y \in W\)
2. スカラー倍について閉じている：\(x \in W\)、\(a\)をスカラーとするなら、\( ax \in W\)

の両方が成り立つことです。

部分空間であることを示すには、まず部分集合であることを示す必要があります。要素が集合に属すること、部分集合であることの証明ができるのは重要な能力です。大学1年生のときの僕は、これがきちんとできていなかった気がします。

参考：集合の要素、部分集合、等しいことの証明の書き方

今回の記事では、既に部分集合であることを示す方法は知っているとして、演算について閉じていることにフォーカスして説明していきます。

部分空間の例と証明

部分空間とはどういうものか、具体的に見ていきましょう。

2，3次元の例

最も簡単な例は、ユークリッド空間\(\mathbb{R}^ N\)の部分空間です。

\(V= \mathbb{R}^2\)における部分空間を考えましょう。

\(W_1 := \{ (x_1,x_2) \mid x_2 =2x_1\}\)と置きます。幾何学的にイメージすれば、これは平面における直線の集合ですね。

\(W_1 \)は\(\mathbb{R}^2\)の部分集合です。さらに、部分空間であることを確かめてみましょう。

まず、和について閉じているかどうかです。\(W_1\)から任意に2つの要素\(x,y\)を選んできます。それは\(W_1\)の要素なので、\(x=(x_1,2x_1)\)、\(y=(y_1,2y_1)\)を満たします。それらの和は、\(x+y=(x_1+y_1,2(x_1+y_1))\)です。第2成分が第1成分の2倍で、\(x+ y \in W_1\)が示せました。

続いて、スカラー倍について閉じているか。\(a \in \mathbb{R}\)、\(x \in W_1\)とすると、\(ax = (ax_1,2a x_1)\)なので、\(ax \in W_1\)です。以上によって、\(W_1\)が部分空間であるとわかりました。

\(W_2 : =\{(x_1,x_2) \mid x_2 =x_1 ^2\}\)と置きましょう。これは放物線のグラフです。

これは部分空間でしょうか？　直線的でなく、どうも部分空間ではなさそうです。

部分空間でないことを示すには、その要素を使って和やスカラー倍を考えると、その外側に出てしまう例があることを示せば良いです。ひとつでも反例が見つかれば、部分空間ではありません。

\(x=(1,1)\)とすると、\(x \in W_2\)です。しかし、そのスカラー倍\(2x\)を考えると、\(2x =(2,2)\)で、\(2 \neq 2^2\)なので、\(2x \not \in W_2\)です。よって、\(W_2\)は部分空間でないと言えました。

舞台を\(\mathbb{R}^3\)に移しましょう。

\(W_3: = \{(x_1,x_2,x_2) \mid 2x_1+3x_2 +x_3 =1\}\)は部分空間でしょうか？

これは部分空間ではありません。\((1,-1,2) \in W_3\)ですが、\(0(1,-1,2) =(0,0,0) \not \in W_3\)なので。0倍というスカラー倍を考えれば、部分空間は必ずゼロベクトル（原点）を含まなければならないことがわかります。ゼロベクトルを含まないなら、即座に部分空間でないと言えるわけですね。これは線形写像かどうかの判定と良く似ています。

参考：線形写像かどうか調べる方法をわかりやすく解説

\(W_4: = \{(x_1,x_2,x_3) \mid 2x_1+3x_2 +x_3 =0\}\)は部分空間でしょうか。

部分空間であることを確かめます。

和とスカラー倍は、\(x+y = (x_1+y_1,x_2+y_2,x_3+y_3)\)、\(ax =(ax_1,ax_2,ax_3)\)です。これが\(W_4\)の方程式を満たすことを確かめましょう。

\[ \begin{aligned} &2(x_1+y_1)+3(x_1+y_2)+(x_3+y_3)\\&= 2x_1+3x_2+x_3 +2y_1+3y_2 +y_3 \\&= 0\end{aligned} \]

\[ \begin{aligned} &2(ax_1)+3(ax_2)+ax_3 \\&= a(2x_1+3x_2+x_3) \\&= 0\end{aligned} \]

よって、\(x+y ,ax \in W_4\)で、\(W_4\)が\(\mathbb{R}^3\)の部分空間であるとわかりました。幾何学的には、これは平面の集合です。

参考：2x+3y+z=0 – Wolframalpha

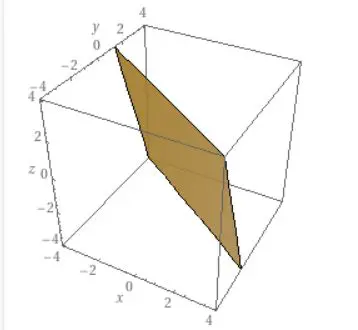
部分空間とは、直線や平面のようにまっすぐと伸ばしていける性質を持った集合のことと言えます。そこは和とスカラー倍について閉じているので、定数倍して伸ばしたり、2つのベクトルの和を使って平面を作ったりできるわけです。

行列の核、像による部分空間

代数的には、\(W_4: = \{(x_1,x_2,x_3) \mid 2x_1+3x_2 +x_3 =0\}\)のように、「多変数の連立1次式＝0」により定まる集合は、部分空間となります。

もっと言えば、必ずそれは\(Ax =0\)と行列により表せるのです。今回のケースならば、

\[ \begin{aligned}A = \begin{pmatrix} 2&0&0\\ 0&3&0\\0&0&1 \end{pmatrix}\end{aligned} \]

、\(x=(x_1,x_2,x_3)\)と置けば、\(W_4 = \{x \mid Ax =0\}\)と表せます。

一般に、\(x=(x_1,\dots,x_N) \in \mathbb{R}^N\)、\(A\)を\(N\)次の正方行列とすると、\(Ax= 0\)は（\(N\)個の）連立一次方程式です。

そして、\(W_5 := \{ x \mid Ax =0\}\)は必ず部分空間となります（これを行列\(A\)の核、ゼロ空間という）。

参考：線形写像の核とは・性質、線形方程式の不定性を調べる

確かめてみましょう。行列については、一般に\(A(x+y)=Ax+Ay\)、\(A(ax)= a Ax\)という性質が成り立ちます（行列は線形写像）。もし\(x,y \in W_5\)ならば、\(A(x+y)=Ax+Ay =0\)、\(A(ax)=a Ax =a0 =0\)なので、\(x+y,ax \in W_5\)。よって、\(W_5\)は部分空間です。

線形写像による（線形空間の）像も、必ず部分空間になることが知られています。

参考：線形方程式と線形写像の像、次元とランクの関係

\(A\)を\(N\)次の正方行列、\(W \)を\(\mathbb{R}^N\)の部分空間とし、\(A(W):=\{y \mid あるx \in W により y=Ax と表せる\}\)としましょう（これを\(A\)による\(W\)の像という）。

\(A(W) \subset \mathbb{R}^ N\)ですが、これが部分空間となることを示します。\(x,y \in A(W)\)とすると、\(Az =x, Aw=y\)を満たす\(z,w \in W\)が存在します。\(W\)は部分空間なので、\(z+w \in W\)です。\(A\)の線形性より、\(A(z+w)=Az+Aw =x+y\)です。よって、\(x+y \in A(W)\)と言えます。スカラー倍についても、\(W\)は部分空間なので\(az \in W\)。\(A\)の線形性より、\(A(az)=aAz =a x\)。よって\(ax \in A(W)\)で、\(A(W)\)が部分空間と言えました。

行列空間

ユークリッド空間以外の部分空間を、いくつか簡単に見ていきましょう。

\(M(N)\)を\(N\)次の実正方行列の集合とすると、それは行列の和とスカラー倍によって線形空間となります。

例えば、対称行列の和、スカラー倍はまた対称行列になります。すなわち、対称行列の集合\(\mathrm{Sym}\)は部分空間です。

可逆行列の集合を\(GL(N)\)とします。それは部分空間となるでしょうか？

なりません。ゼロベクトル、\(M(N)\)においてはゼロ行列\(O\)を含まないからです。\(O\)は可逆行列ではありません。\( O \not \in GL(N)\)なので、\(GL(N)\)は部分空間ではないと言えます。

数列空間

実数列全体の集合\(\ell (\mathbb{N})\)は、数列の和とスカラー倍について、線形空間となります。

\(W_6\)を等差数列全体のなす集合とします。これは部分空間でしょうか。

部分空間です。等差数列は、\(x_n =d_1 (n-1)+x_1\)、\(y_n =d_2 (n-1)+y_1\)と表せます。その和は、\(x_n+y_n = (d_1+d_2)(n-1)+(x_1+y_1)\)と表せるので等差数列です。スカラー倍も、\(ax_n = ad_1(n-1)+ax_1\)と表せるのので、等差数列です。

では、等比数列全体のなす集合\(W_7\)は、部分空間でしょうか。

こちらは部分空間ではありません。例えば、\(x_n =2^{n-1}\)、\(y_n =3^{n-1}\)という等比数列を考えます。その和は等比数列ではありません。隣り合う項の比を取ると、\(\frac{x_{n+1}+y_{n+1}}{x_n+y_n}=\frac{2^n+3^n}{2^{n-1}+3^{n-1}}\)です。\(n=1\)のときは\(\frac{5}{2}\)、\(n=2\)のときは\(\frac{13}{5}\)と、比が一定でないので等比数列ではありません。

関数空間

連続関数のなす集合\(C(\mathbb{R})\)や可積分関数のなす集合\(L^p(\mathbb{R})\)は、関数の和、スカラー倍について線形空間となっています（関数空間）。

\(N\)次の多項式関数のなす集合\(P_N(\mathbb{R})\)は、\(C(\mathbb{R})\)の部分空間でしょうか。多項式関数は連続なので、連続関数の集合の部分集合となっています。

部分空間です。\(a_N x^N +\cdots +a_1x+a_0\)と\(b_N x^N +\cdots +b_1x+b_0\)の和は、\((a_N+b_N)x^ N +\cdots +(a_1+b_1)x +(a_0+b_0)\)と\(N\)次の多項式になっています。スカラー倍も、\(\lambda a_N x^N+\cdots +\lambda a_1 x+\lambda a_0\)と\(N\)次多項式ですね。

不連続な可積分関数のなす集合\(W_8\)は、区間\([-1,1]\)で定義された可積分関数のなす空間\(L^1([-1,1])\)の部分空間でしょうか。

部分空間ではありません。

\[ \begin{aligned}f(x)= \begin{cases}0 & (-1 \leq x <0 )\\1 & (0 \leq x \leq 1)\end{cases}\end{aligned} \]

\[ \begin{aligned}g(x)= \begin{cases}1 & (-1 \leq x <0 )\\0 & (0 \leq x \leq 1)\end{cases}\end{aligned} \]

とすると、\(f,g\)は原点で不連続で、可積分です。しかし、その和は\(f+g (x)=1\)となる定値関数で、連続です。よって、\(W_8\)は部分空間ではありません。

以上、部分空間とは何か、低次元の例やさまざまな例、証明の書き方を紹介してきました。

部分空間とは、和とスカラー倍について閉じた部分集合のことです。

\(W\)の要素の和やスカラー倍を具体的にイメージして、部分空間であるかどうか予想をつける。
1. 違うならば、和やスカラー倍について閉じていない反例を挙げる。
  1. 0ベクトルを含まないならば、部分空間ではない。
2. 部分空間っぽいならば、次のステップへ進む。
部分集合であることを確かめる
\(W\)の要素\(x,y\)を任意に選んで、その和\(x+y\)を計算する。それが再び\(W\)の要素となるか調べる。
\(W\)の要素\(x\)とスカラー\(a\)を任意に選んで、\(ax\)を計算する。それが再び\(W\)の要素となるか調べる。

幾何学的にイメージをするのも大事ですが、予想をつけたら部分空間の定義を満たすことを確かめる必要があります。

何が仮定で、何が定義で、何が示したいことなのか。順を追って示せるようになってみてください。

木村すらいむ（@kimu3_slime）でした。ではでは。