どうも、木村(@kimu3_slime)です。
高校数学のベクトルの分野では、ベクトルの内積というものを考えますが、なぜそれでコサインが登場するのか戸惑った記憶があります。
今回は、余弦定理をベースにして、ベクトルの内積の表示式に納得できる説明を簡単に与えたいと思います。
余弦定理とは
余弦定理とは、三角形の3つの辺の長さと角度の関係を表した定理です。
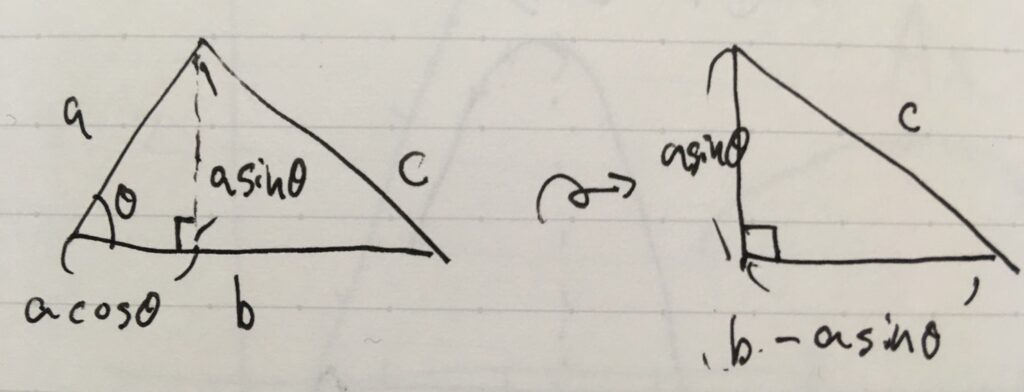
3つの辺の長さを\(a,b,c\)、長さ\(a,b\)の辺のなす角度を\(\theta \)とすると、
\[ \begin{aligned}a^2 +b^ 2 -2ab \cos \theta = c^2\end{aligned} \]
というものです。2つの辺が挟んでいる角度のコサイン\(\cos \theta\)が登場しますね。
余弦定理というとなんだか難しそうに聞こえますが、これは三平方の定理(ピタゴラスの定理)
\[ \begin{aligned}a^2+b^2 = c^2\end{aligned} \]
の拡張にすぎません。
実際、上の図から三平方の定理を使って、余弦定理を証明しましょう。
頂点から長さ\(b\)の辺に垂線を下ろすと、三角関数の定義より隣り合う辺の長さが\(a\sin \theta, a \cos \theta\)といったように求められます。したがって、右側に斜辺が\(c\)、他の2辺が\(a\sin \theta, b- a\cos \theta\)である直角三角形ができあがります。
直角三角形については三平方の定理が使えるので、
\[ \begin{aligned}(a \sin \theta)^2 + (b-a \cos \theta)^2 = c^2\end{aligned} \]
で、左辺は
\[ \begin{aligned} &a^2 (\sin \theta )^2 +b^2 -2ab\cos \theta + a^2 (\cos \theta)^2 \\&= a^2 ((\sin \theta )^2+ (\cos \theta)^2)+b^2 -2ab\cos \theta \\ &= a^ 2+b^2 -2ab \cos \theta \end{aligned} \]
となります(三角関数の性質:\((\sin \theta )^2+ (\cos \theta)^2=1\)を用いた)。よって、余弦定理が成り立つことがわかりました。
特に、余弦定理で\(\theta = 90 ^{\circ}= \frac{\pi}{2}\)のとき、\(\cos \theta =0\)なので、三平方の定理の形になっていますね。一般には、なす角度に応じて\(-2ab \cos \theta\)分の補正をする必要があるわけです。
ベクトルの内積と余弦定理の関係
さて、話をベクトルの内積にうつしましょう。特に平面におけるベクトルを考えます。
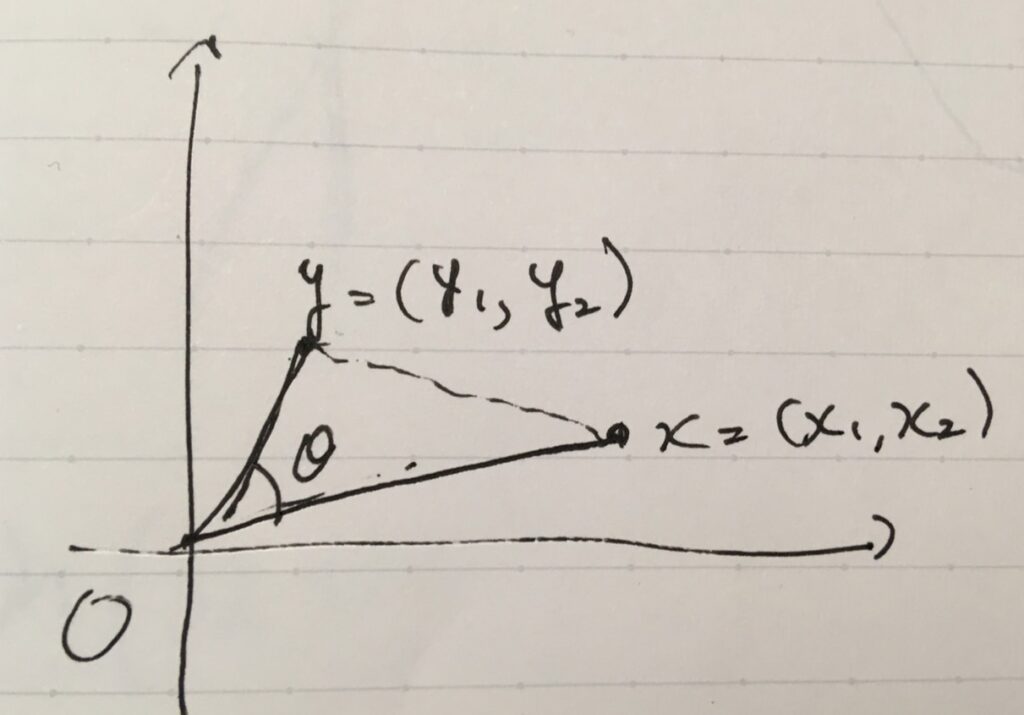
2つのベクトルを\(x,y\)として、その成分を\(x=(x_1,x_2)\)、\(y= (y_1,y_2)\)と一般的に表しましょう。高校の教科書では、ベクトルを\(\vec{x}\)や\(\vec{OX}\)と書くかもしれませんが、矢印の飾りがなくても同じです。
ベクトルの内積(inner product)は、
\[ \begin{aligned}\langle x,y\rangle := x_1y_1+x_2y_2\end{aligned} \]
と定義します。左辺は\(\vec{x}\cdot \vec{y}\)と書いても同じです。内積という計算を意識しやすい表記法にしました。
例えば、\(x= (2,0)\)、\(y=(3,1)\)ならば、\(\langle x,y\rangle = 2\cdot 3 +0\cdot 1 =6\)です。
この定義では、ベクトルの内積は、第一成分の積と第二成分の積を足し合わせたものです。
なぜこんなものを考えるかはともかく、計算は単純で、「内積」と積っぽい用語をつけることには納得できるでしょう。
内積には、もうひとつ別の表示式、計算方法があります。
\[ \begin{aligned}\langle x,y\rangle = \|x\| \|y\| \cos \theta\end{aligned} \]
です。ここで\(\theta\)は\(x,y\)のなす角度で、\(\|x\|\)はベクトルの大きさを表します。三平方の定理によって具体的表せば、\(\|x\| = \sqrt{x_1 ^2 +x_2 ^2}\)です。
高校数学の教科書の流れによっては、まずコサインを使った内積を学び、その後にそれが成分の積に等しいことを学ぶでしょう。
どちらを定義と考えても良いですが、ポイントは、一見異なるように見える2つの式が等しいこと
\[ \begin{aligned} x_1y_1+x_2y_2 = \|x\| \|y\| \cos \theta\end{aligned} \]
です。
この等式が成り立つことを確かめるために、余弦定理を利用しましょう。
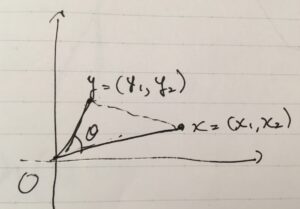
余弦定理の記号で言えば、3つの辺の長さは、\(a= \|x\|\)、\(b= \|y\|\)、\(c= \| x-y\|\)に対応しています。このときの余弦定理は、
\[ \begin{aligned}\|x\|^2 +\|y\|^2 -2 \|x\| \|y\| \cos \theta = \|x-y\|^2\end{aligned} \]
ですね。ここから内積の式の形を取り出すと
\[ \begin{aligned}\|x\| \|y\| \cos \theta = \frac{1}{2}(\|x\|^2 +\|y\|^2 -\|x-y\|^2)\end{aligned} \]
となります。右辺を計算していけば、
\[ \begin{aligned} &\frac{1}{2}(\|x\|^2 +\|y\|^2 -\|x-y\|^2) \\&= \frac{1}{2} (x_1^2+x_2 ^2 +y_1^2 +y_2^2\\ &-(x_1-y_1)^2-(x_2-y_2)^2 ) \\ &= \frac{1}{2}(2x_1y_1 +2x_2 y_2) \\ &=x_1y_1 +x_2y_2\end{aligned} \]
と求める関係式が得られました。
内積の関係式を使えば、
\[ \begin{aligned}\cos \theta =\frac{\langle x,y\rangle }{ \|x\| \|y\| }\end{aligned} \]
と機械的に2つのベクトルのなす角度(のコサイン)を計算することができます。
より一般には、\(3,4\)次元以上の一般的なベクトルや、関数に対しても、内積を通じてその「角度」という幾何学的な見方を手に入れることができます。それが内積を考える意義のひとつです。
参考:ユークリッド空間R^Nの内積、ノルム、距離について解説
以上、ベクトルの内積になぜコサインが登場するか、余弦定理と関連させて紹介してきました。
ベクトルのなす角度を捉えようとすると、そこに三角形ができあがり、余弦定理による関係式が登場してきます。余弦定理は、三平方の定理のような三角形に関する基本的な定理です。だからコサインが登場する、という説明で納得できるでしょうか。
用語としてはサイン、コサインという名称がついていて、コサインは2番目……というような印象を抱きがちかもしれません。しかし内積に限らず、極座標やバネの振動、オイラーの公式、フーリエ級数など、コサインが先に登場することの方が多いです。
この記事を通して、むしろコサインは基本的な三角関数である、という印象も持ってもらえたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。