どうも、木村(@kimu3_slime)です。
算数や数学の学習の場で、生徒の質問に対し、「そういうものだ」「そう決まっているのだ」と指導者・先生が答えるケースがあることを知りました。良くないことです。
今回はそんな回答をされたときに、学ぶ側(生徒)はどう対処すれば良いか、そんな話をします。
「そう決まっている」は思考の放棄
「そう決まっている」という言葉は、小学校や中学校でよく使われている記憶があります。ここでは、具体的な例を紹介しましょう。
担任の先生が「タイルが10個集まったら『棒』になるんだよ。それが十だよ。」と言い,多くの子どもたちはうなずくようにしていたが,指導の難しい子どもとして観察を依頼されていた高機能自閉症と診断されているAくんが突然手を上げ「先生,どうしてタイルが10個集まると棒になるの?9個じゃならないの?11個じゃならないの?5個だって棒になるよ,ほら。」と言って机にタイルを5個並べた。この文章をお読みの先生方ならAくんに何と答えてあげるのだろう。担任の先生は「そう決まってるの!」と,またかという顔をして断言。
参考:特別支援教育から見た小学校1学年の算数 – 玉川大学教職大学院 准教授 阿久澤 栄
「9個だって11個だって5個だって棒になる。」この生徒は、とても良い指摘をしていると僕は思います。
これに対して「そう決まっているの!」と答えるのは、「決まっていること」それそのものは間違いではないのですが、「何が決まっているのか」「どうしてそういう決まりを考えるのか」の説明が不十分です。
僕ならばこう答えるでしょう。
まず、それは良い質問です。9でも11でも5でも棒は作れます。例えば、時計(分)では60を1つの棒(単位)と考えていますね。
普通の数では10を基準にすることがが多く、時間や角度では60を基準にすることが多いです。これは絶対に定まったことではなく、かつて人が数というものを見出してから、歴史的に受け継がれてきたものです。
10が選ばれた理由のひとつは、指の数に由来するという説が考えられますね。これから学ぶように、10を基準にする位取り法は、足し算やかけ算などの計算がしやすいことが知られています。
算数の授業では、最初に10を基準に数を捉えていくことを学びます。でも、「別の基準で数を捉える」という考え方は本当に良いものです。これは60進法や2進法、n進法といった世界につながります(いつか自分で学んでみてね)。
実際的には、集団授業という形式がそもそも説明不足を招く面があります。曰く、こんなに詳しく話す時間がない。逆に言えば、多数の理解を優先するという名目で、「そういうものだ」式の説明で押し通してしまう先生がいる、というのも現状でしょう。
おそらく、先生自身も、「なぜそうなっているかわからない」「なぜこれを教えるのかわからない」と思う人が少なくないのでしょう。先生も一人の人間ですから、わからないことは当然あります。
問題は、わからないことそのものではなく、それをごまかして「そう決められている」と生徒の疑問をつっぱねてしまうことにあります。「良い質問だね。先生でもすぐには答えられないよ。」と誠実に答えてあげれば良いだけのことでしょう。
学ぶときの態度を理解していないのか、教師としてのプライドなのか、「決まっている」と権威的に答えてしまうのは残念です。僕はそうした先生を見て、子どもながらに、「この先生は、おそらく説明ができるほど理解していないのだ」と見限っていました。
「そういうものだ」という態度のは、生徒の疑問に対する回答の放棄であり、思考の放棄だと思います。考えることをやめている人から、何かを学びたいとは、僕は思いません。
数学という学問は、ほかの自然科学や人文学に比べて、「そういうものだ」式の説明でなく、自己完結で理屈を教えやすいにもかかわらず、「そういうものだ」式の教え方がされやすいようです。
生徒の話。
相加相乗使って最小値求める問題でなぜ等号成立を確認するのか、わざわざ学校の先生に質問に行ったら
「そう書いてあるし、これはそういうもんだって覚えて」
と教えていただいたそうです。
— 大北あきや(数学講師) (@akiyaokita) February 12, 2021
参考:不等式の証明で等号成立を確かめる必要がないのはなぜか:≦の意味
「そういうものだ」と丸暗記するタイプの勉強は、(普通は)限界があり、応用がききません。できるだけ理屈をつけて、納得しながら進むのが、勉強のコツです。
決まりごとと法則を区別する
「そんなの決まってるよ。当たり前だよ」と考える先生がいることは、仕方のないことです。集団授業は大変ですし、授業の準備をする余裕のない環境もあるでしょう。
とはいえ学ぶ側からすれば、「決まってるよ」と言われたら、何のために学校があるのかわかりません。「じゃあ塾に行きますよ」と良い先生のあてがあるなら良いですが、そうでない人も多いはずです。
じゃあどうすれば良いのか。自分で考えて整理するしかありません。
そこで大事なのが、決まりごとと法則を区別することです。少し難しい言い方をすれば、定義と定理と経験法則を区別すること。
定義とは、言葉の意味を限定することです。「どうして2の倍数のことを偶数と呼ぶの?」と言われたら、それは定義(約束)だから、としか答えようがありません。「2の倍数のことを、偶数と呼ぶことにしましょう。」と、数学を学ぶ人の間で共通認識を作っているのです。「サッカーでどうして手を使ってはいけないの」というのは、それが(みんなで決めた)ルールだからです。
実は定義やルール以外のものも、「決められたことだよ」という人がはよくいます。僕はそれを「決められたこと」というのは不適切だと思いますが。
例えば「どうして4の倍数は偶数でもあるの?」という問いに、「(4の倍数は偶数と)決まっているよ」と答えるのは不適切です。これは定理や命題と呼ばれる、数学的な事実です。それは定義から導かれる性質のことであり、その導き方を記す文章は証明と呼ばれています。「事実が確定している(真偽がはっきりしている)」ことは、「ルールをそう取り決めた」こととは別物なのです。
問題の解き方で変わった工夫をしているのを見て、どうしてこうするのかわからない、なのに「決まっている」と教師が説明することもあるでしょう。数学的な事実の示し方は一通りではなく、「決まっている」なんてことはありません。工夫のひとつとして、なぜそれがうまくいっているのか、他の例を考えたりして考えてみましょう(これはすごく勉強になります)。
数学を少し離れると、経験法則、実験法則があります。
例えば「りんごが木から落ちる」ということは、経験的に知られた事実です。物体の運動全般に成り立つ事実は、まとめて物理法則として説明されます。「質量のある物体の間には万有引力が働く」ことは、高校レベルの物理で、ひとつの回答です。
しかしさらに、「どうして万有引力なんてものがあるか」を答えられる先生は少ないでしょう(僕はよく知らないです)。こういう問題は、「世界はそういう風にできている。なぜかはわからない。」と僕なら答えます。良い疑問なので、もし興味があれば、ぜひ大学に進学で学び、いつか教えてほしい、と頼むでしょう。
以上をまとめれば、「決まっている」という言葉の意味は
- 定義:言葉の取り決めとして「決まっている」
- 定理:定義から導かれる性質として「決まっている」
- 経験法則:数多くの経験により「決まっている」(ように見える)
の3種類に分かれます。学びの中で疑問が生まれて、「当たり前に決まっている」と感じたら、上のどれに当てはまるのか考えてみてはいかがでしょうか。
(これらの区別がはっきりする人が多くないのは、数学教育の問題点だと思っています。物事を順を追って人に納得させられるように述べる力、論証力が重視されるようになってほしいです。)
「そういうものだと受け入れる」は最終手段
とはいえ、学校教育の中で、「なぜ?なぜ?」と考えていると、いつまでたっても先に進めないという問題が生まれてきます。
僕は自分の理解のペースで考えていくことが、学びを続ける上では大事だと思っています。が、日本の社会(例えば学校や塾)は、学年=学習内容と言わんばかりに、一定のペースで学ぶことを薦めてくるものです。
そんな中で生まれてくる方便が、「そういうものだと覚える」です。
「円周率は3.14」ってことを「そういうもの」として覚えているんです。
引用:【教科別】数学の勉強で「この問題なんでこうなるの?」の対処法! – 武田塾
「定義(言葉の約束)をそういうものだと覚える」ことは、僕は否定しません。それは覚えなければ、議論の土台に立てないからです。しかし、定義ではないものを覚えようとすることは、ほとんど思考の放棄に近く、おすすめできません。
例えば「円周率は3.14」と覚えさせるのは、テスト・試験の点数を取らせるための方便です。僕は楽しくて円周率の暗記ゲームをしていましたが、そんなことをする必要は全くないと思います。「およそ3」で良いのです。
「そういうものだと覚える」で覚えられたら、学ぶ側は苦労しません。覚えるので納得できないから、考えるし、学問があるのではないでしょうか。覚えることに慣れきってしまえば、「人から言われたことを覚える」人生を送ることにつながります。考えるという武器を手放すことにつながるのです。子どもが持っている考える能力をくじくのは、やめた方が良いと思います。
では、覚えずに考えるにはどうしたらいいか。
さきほどの例で言えば、円周率の定義を知ること、円周率とは何かをまず答えられるようにすることです。答えられますか? それは、円を考えたときに、直径を基準とした円周の長さ(割合)のこと(\(\pi = \frac{\ell}{2r}\))です。この定義が答えられた上で、その値がおよそ3.14であることを、一般に知られたものと「覚える」のは良いでしょう。
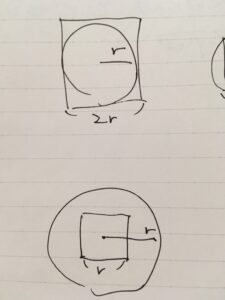
ただし、その値になる理屈はあります。実際に、図を書いたりものを作って、計測してみるのも良いでしょう。
例えば半径\(r\)の円に外接する四角形(正方形)を考えれば、その周の長さは\(2r \times 4 =8r\)で、その比は\(\frac{8r}{2r}=4\)です。円周は少なくともこの四角形の周長より短いので、\(\pi <4\)がわかります。同様にして、円の内側に周の長さが\(4r\)である正方形はいつでも存在します。そこから\(2<\pi\)がわかります。これらから、\(2< \pi <4\)なのだな、というあたりはつけられるのです。
(正確には、周の長さを比較する議論は微妙です。厳密には、円の面積\(\pi r^2\)と四角形の面積\(4r^2\)を比較して議論しているといった方が適切でしょう)
2003年の東京大学の入試問題「円周率が3.05より大きいことを証明せよ」は有名です。上で述べたような考え方、内接多角形による近似を考えれば、導くことができます。
円周率の値を覚える(知っている)だけでなく、なぜその値になるかには理屈がありますよ、それを説明できますか、と問うているわけですね。
もちろん最終的には、「そういうものだと受け入れる」と思って先に進むこともあるでしょう。公式をとりあえず覚えて、駆使して計算してみるのは大事なことです。
ただしそれを最終手段だと思わずに、「勉強は、決まっていることを覚えるんだ」と思ってしまったら、何も楽しくないですし、それは長期的に勉強自体を苦手に、嫌いにしていくと思います。
逆に言えば、「どうしてこうっているのだろう?」「決まっていると人は言うが、どうしてそう決まっているのだろう」と考えて、自分のペースでその答えを導く過程は、とても楽しいものです。
以上、算数・数学における「そういうものだ」への対処法を紹介してきました。
理屈をつけて考えることは、大変ですが面白いことです。微妙な教え方に出会ったとしても、めげずに考えてみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。