どうも、木村(@kimu3_slime)です。
今回は、重積分とは何か、その逐次積分による計算方法(フビニの定理)を簡単に紹介します。
重積分とは
場所によって密度が違うプレート(平板)の重さ、場所によって熱量が違う空間の総熱量など、平面や空間における関数の総和を調べるのが重積分です。
続いて重積分の定義を紹介します。なんだか複雑な定義と思うかもしれませんが、計算方法は後で紹介するので安心してください。
簡単のため、平面\(\mathbb{R}^2\)における2変数関数について考えましょう。
積分範囲は、1次元の積分では区間\([a,b]\)を考えました。2次元ではさまざまな形が考えられますが、長方形\(D=[a,b]\times [c,d]\)における積分を考えてみます。
1次元の積分では、例えば区間\([0,1]\)を幅\(\frac{1}{n}\)で細かくわけていって、幅×関数\(\frac{1}{n}f(x_k) \)の和を積分の近似値として捉えました。その分割を細かくしていったときに近づく値が、積分値です。
2次元では、例えば区間\([0,1]\times[0,1]\)を、面積\(\frac{1}{n^2}\)の細かい正方形\(S_{k,\ell}\)に分けて、そこにおける\(\frac{1}{n^2} f(x_k,y_k)\)の和を重積分の近似値と呼ぶことにします。その分割を小さくしていったときに近づく値を、\(f\)の重積分(multiple integral)と呼び、
\[ \begin{aligned}\int _D f ,\quad \int _D f(x,y)dxdy\end{aligned} \]
と書きます。
定数関数\(f(x,y)=1\)の\(D=[a,b]\times [c,d]\)における重積分を計算してみます。\([a,b],[c,d]\)をそれぞれ\(n\)等分した長方形\(S_{k,\ell}\)を考えると、1辺の長さは\(\frac{1}{n}(b-a),\frac{1}{n}(d-c)\)なので、その面積は\(\frac{1}{n^2} (b-a)(d-c)\)です。
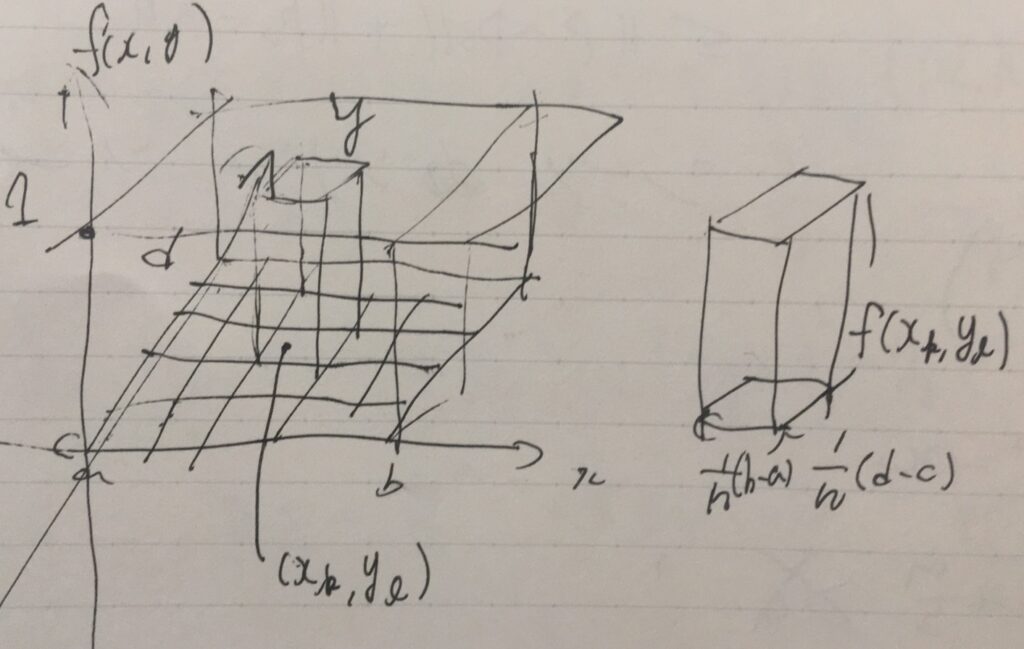
積分を近似する和は、細かい長方形の面積×そこにおける関数値\(f(x_k,y_k)\)の足し合わせなので、
\[ \begin{aligned}\sum _{k=1}^{n} \sum _{\ell =1}^{n} \frac{1}{n^2}(b-a)(d-c) f(x_k,y_\ell)\\=\sum _{k=1}^{n} \sum _{\ell =1}^{n} \frac{1}{n^2}(b-a)(d-c) = (b-a)(d-c)\end{aligned} \]
です。よって、
\[ \begin{aligned}\int _D f =\lim_{n\to \infty }\sum _{k=1}^{n} \sum _{\ell =1}^{n} \frac{1}{n^2}(b-a)(d-c) f(x_k,y_\ell) \\=(b-a)(d-c)\end{aligned} \]
となりました。これは長方形\(D\)の面積ですね。
1次元の区間\([a,b]\)における1の積分は、その長さ\(b-a\)を返しますが、それと同じです。3次元の重積分ならば、立方体の体積を返します。(むしろ、この積分の値をもって、面積や体積を定義している)
1次元の積分は長方形近似と言えますが、2次元の積分は立方体での近似です。
区間の分割の仕方を均等でないようなものを考えると、一般には積分近似値の極限は変わってしまいます。どんな近似の仕方を考えても、積分近似値の極限が変わらないとき、その関数を可積分といいます。連続関数は可積分であることが知られているため、区間の分け方を気にしなくて良いのです。
また、\(D\)は区間の直積でなくても、円や球の内部、一般には有界な集合における積分も考えられます。その有界な集合を含む長方形を考え、\(D\)においては\(f\)、\(D\)以外の点においては0の値を取る関数の重積分を考えれば良いです。
逐次積分による計算法
重積分を定義によって計算するのは、一般には難しいです。
1次元の積分では、定義による計算よりは、原始関数を使った計算が普通でした。重積分でも、1次元の積分の繰り返しとして計算できるという性質があり、原始関数を使った計算に帰着されます。
フビニの定理
\(D\subset \mathbb{R}^N\)を有界な集合、\(D=I\times J\)、\(f:I\times J \to \mathbb{R}\)を連続な関数とする。このとき、
\[ \begin{aligned}\int_ D f = \int _I (\int _J f(x,y)dy)dx = \int_J(\int _I f(x,y)dx)dy\end{aligned} \]
が成り立つ。
右辺の積分は、\(y\)について積分してから\(x\)について積分している(逆も同様)ので、逐次積分、反復積分(repeated integral)と呼ばれます。
試しに、\(f(x,y)=1-(x^2+y^2)\)を\(D=[0,1]\times [0,1]\)において重積分してみましょう。
有界な集合上で連続な関数なので、フビニの定理が適用でき、類似積分として計算できます。
\[ \begin{aligned} \int_D f &=\int_0^1 (\int_0^1 (1-(x^2+y^2)dy)dx \\ &=\int_0^1 [(1-x^2)y -\frac{1}{3}y^3]_0 ^1 dx \\ &=\int_0^1 (\frac{2}{3}-x^2)dx \\ &=[\frac{2}{3}x -\frac{1}{3}x^3]_0 ^1 \\ &= \frac{1}{3} \end{aligned} \]
となりました。
\(f\)を密度関数と捉えれば、この重積分は\(D\)における重さを求めたということになります。
一般に、\(f\)の\(x\)方向の重心(center of mass)は、各位置\(x\)における重さ\(xf(x,y)\)を全体の重さで割ったものとして定義されます。
\[ \begin{aligned}\bar{x}:= \frac{\int _D xf(x,y) dx dy}{\int _D f(x,y) dx dy}\end{aligned} \]
\(f(x,y)=1-(x^2+y^2)\)について、重心を求めてみましょう。
\[ \begin{aligned} \int_D xf &=\int_0^1 x(\int_0^1 (1-(x^2+y^2)dy)dx \\ &=\int_0^1 (\frac{2}{3}x-x^3)dx \\ &=[\frac{1}{3}x^2 -\frac{1}{4}x^4]_0 ^1 \\ &= \frac{1}{12} \end{aligned} \]
なので、\(\bar{x}=\frac{\frac{1}{12}}{\frac{1}{3} }=\frac{1}{4}\)と、\([0,1]\)においては原点に寄った重心を持っていることがわかりました。
\(y\)の重心についても、同様の議論ができます。
以上、重積分の定義と、その逐次積分による計算方法(フビニの定理)を紹介してきました。
今回は2次元の例でしたが、3次元以上でも同様の計算ができます。
面積や体積、重さや熱、圧力といった連続的に分布する量の合計を考えると、重積分は自然に登場してきます。熱方程式や波動方程式といった偏微分方程式の理解の基礎ともなっているので、ぜひ身につけてみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店 (1981-11-15T00:00:01Z)
¥5,720
東京大学出版会 (1985-04-25T00:00:01Z)
¥3,740