どうも、木村(@kimu3_slime)です。
「趣味の大学数学」で大学数学の解説記事を書くたびに思うのです。ほんの入口を紹介するのに、どれだけ多くの文量になるかということを。
大学数学の本(数学書)は、高校までの教科書と比べると、難しいことが短いページで述べられていて、ちゃんと読める人がどれだけいるのか……という気持ちになります。
本当は数学書の読み方について書きたいです。しかし、いきなりそれは難しそうなので、数学書が難しいのはなぜか、に注目して分析していきたいと思います。
大学数学が(理論的には)独学できる学問だとしても、数学科に進まなければ数学書を読めるようにならないのだとしたら、実際には限られた人しか独学ができないに等しい。
数学科でなくても独学できるための実際的な考え方や知識を、ネット上の文章で提供できるようになればなと思う。— 木村すらいむ (@kimu3_slime) November 27, 2020
内容が圧縮されている
まず前提として、多くの数学書は難しいものだ、ということを受け入れたほうが良さそうです。簡単な本は少ないです。
数学者の人であっても、「通読が困難」「精読すれば1日1ページ進まないことさえある」と言うほどです。(僕も同じ感想です)
私が数学の本を読むのがあまり得意でないからです。 数学の本は、通常書店に並んでいる本の中で、専門書と いわれるものに限ってみても、やっぱり難しい。 まず、通読することが困難です。困難というのが不適当なら、 非常に時間がかかるのが普通です。 精読すれば、一日に1 ページもすすまないことさえ良くあります。
引用:数学の本はどう読むの? 数せみ1998年4月号・特集「数学ガイダンス」のための原稿
大学で数学を学んだ経験のない人にとっては、なおさら難しいものであると言えるでしょう。つまり、初学者の段階では、わからなくても仕方がないと思います。すぐにわからなかったからといって、原因は頭が悪いからではありません、あきらめないでください(笑)。
数学の本で説明がどれだけ省略されているか、具体的に見てみましょう。
これは齋藤「線型代数入門」の、第1章の1ページ目です。(ちなみに「線型代数入門」は本格的に数学を学びたい人にとっては詳しくて良い本だと思います、僕はこれで線形代数学を学びました。ただし初学者には厳しいと思います。)

引用:齋藤「線型代数入門」
ちなみに、この後はすぐにベクトルの話に変わり、特にこのページで述べられた概念に関する記述はありません。典型的な数学書、という感じがします。これで理解できるのは、すでにある程度学んだ人、既習者だけではないでしょうか。せめて、「集合と写像については、別の本で各自学んでほしい」くらい書いてあれば親切だと思いますが。
「~~入門」という本は、決してやさしい本ではなく、理論の基礎を本格的に学びたい人・学びなおしたい人のための本、という意味あいがあります。
例えばこの本の記述をそのまま板書して、大学生1年生向けに講義したとして、どれだけの人が何を言っているのか理解できるのでしょうか。僕はこのタイプの講義を聞いて、ついていけなくなった経験があります。
参考:大学の数学の勉強についていけなかった経験談、その解決法
この1ページには、集合と写像に関する基本的な概念が短くまとめられています。(一応4章になると集合論の補足説明がありますが)僕にとってはそれは簡潔すぎて説明不足と感じました。後に集合論の教科書を読むことで、やっと納得して読めるようになったのです。自分がもしこのへんの話を講義するとしたら、次のような記事の文量になるでしょう(これでもごく一部ですが)。
参考:集合論入門:集合の定義、数の集合、ラッセルのパラドックス、無限集合の濃度とは? 写像の全単射、可算無限、カントールの対角線論法
それだけ多くの内容が省略されている、ということではないでしょうか。講義ではこの省略が補われるかもしれませんが、独学だとそれを自分で補わなければなりません。
講義の時間数的に、また教科書の紙面の都合上で、短く内容を書かざるを得ない面はあるのでしょうが、それにしても初学者はハードルを感じるでしょう。
具体例がない、少ない
数学書の難しさの要因に、具体例が挙げられていない、あるいは少ない、一般的すぎることがあります。
さきほどの引用においても、具体例が全くありません。高校までの教科書ならば、絶対に簡単な具体例や計算例があります。つまり、具体例がどういうものか、定義を満たすものや満たさないものは何か、定義を確かめるにはどうしたらいいか、読者は自分で考えなければならないのです。
そんなことは数学科の人にとっては当たり前のことですが、そういう本の読み方を、高校まででは教わっていない・身についていないのではないでしょうか。数学科の人は、講義や演習、ゼミを通してだんだんと具体例を考えるスキルを身に着けています。
最初のうちは、教科書とは別に演習書を探して読むのも良いでしょう。例えば、線形代数ならば僕は「基本演習 線形代数」を読んで、具体的な計算に慣れた気がします。
専門的な数学になるほど、演習書のような本は少なくなっていきます。しかしながら、数学を専門とする人は教科書を読みながら、多くの具体例を考えてノートで計算・論証しているはずです。具体例がなくてわかりにくいのならば、自分で作るしかないでしょう。
証明が省略されている、ない、行間が広い
数学書のレベルによっては、ちょっとした命題や例の証明は、省略されています。
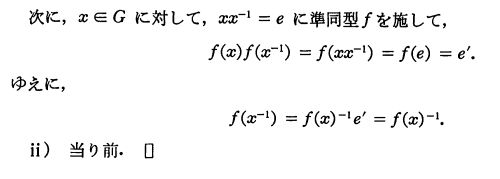
—

「当たり前(自明)」「~から明らか」は、まさに省略を表す文章です。最終的には「当たり前」と思えるようになるべきなのですが、最初からそう思えたなら苦労しません。当たり前と言えるためには、誰でも納得のできる証明を自分で書くスキルが求められています。いわゆる、行間を埋める力が必要です。
参考:「自明、明らかである」に気をつけて、疑いながら数学書を読もう、数学の学びを深めるために必要なのは、「わからない」と言える力
当たり前とすら書かれず、証明が省略されていることはしばしばあります。「この例はあの定義を満たす。」(ただし証明は書いていない)といった形式のもの。

読者は、自分でノートにその証明を書けるよう努力したほうが良いでしょう。それができないと、本の中身についていくのは相当しんどいと思います。
多くの詳細な証明を語らず、深い内容をコンパクトに紹介する数学書も、格調高くてそれはそれで僕は好きです。ある分野を深く理解して、俯瞰的に眺めるのも大事です。しかし、初学者が地に足のついた理解をするには、証明の省略が多い本はスパルタだと思います。
天下りの話の展開になりがち
数学書は、話の展開の仕方も、高校までの教科書とは違う部分があります。それは、抽象的で一般的な定義から議論を始めることです。

引用:杉浦「解析入門1」
厳密に議論しようとすると、基礎的な概念は最初に紹介しなければなりません。公理的なアプローチで、直観に頼る図も少なく、論証のみによって話を進めていくスタイルは、ブルバキスタイルと呼ばれるものです。
参考:なぜ教養数学として微積分学と線形代数学を学ぶのか ブルバキが現代数学に与えた影響
確かに、数学に慣れ親しんだ人にとっては、厳密であることがわかりやすさになる面があります。曖昧な議論が最初に登場すると、これの定義は何なのだ、と戸惑うわけです。
しかしながら、数学の初学者は、なぜこうした定義を行うのだろう、何のために長々と厳密に議論しているのだろう、と疑問に思うことがあるのではないでしょうか。おおざっぱな気持ちやイメージを知りたくても、多くの数学書は厳密性を重視するあまりフィーリングを排除しています。「後の議論に必要だから」と天下り式に学ばなければならないのが、退屈だと思うこともあるはずです。
「定義は定義なのだから、そういうものだと思って受け入れるしかない」という数学の学び方をしている人はいるかもしれません。ある意味では正しいです。公理的な定義がどうやって役立つかは、すぐにはわかりません。その本を読み終わるぐらいまで進んでようやく、基礎が大事であったことに気づいたりします。
論理的に正しい順序が初学者が理解しやすい順序とは限らないので、天下りっぽいと感じたら、順序を無視して後半部分を読んでみると良いでしょう。
目的・目標や問題、応用が最初に示されない
さきほどの論点と似ていますが、数学書はその目標や応用を本文中で書き表さないことが多いです。良いプレゼンテーションのようなわかりやすさがありません。

引用:黒田「関数解析」
「基礎的な内容だから一通り身につける」のは、数学の一般性ゆえに仕方がないことかもしれませんが、目的が曖昧です。一般論そのものを目的とした本は、数学を専門とする人以外に興味を持ってもらうのは難しいと思います。基礎学問とはそういうものなのかもしれませんが……。
章の頭から「~を~とする。このとき~が成り立つ」と、この章で何をしたいかが書かれていないことは珍しくありません。例えば上の引用において、「関数解析的方法の有効性」が示されるのは冒頭から100ページ後です。途中でDirichlet問題がどういう問題かは述べられますが、それにどんな意義があるのか、どう面白いのかは書かれていません。
数学書によくあることですが、まえがきではイメージや話題が提示されるのですが、本文が始まるとミクロな数学の中身のことばかりで、まるで全体像の話や歴史的経緯の話がなかったりします。
この点に関して、「ストラング:線形代数イントロダクション」は意義付けを感じやすい本です。各節の最初に何を主張しているか短くまとめがあって、文章の始まりとしても「この節は~に関するもので、~~が重要である」と書かれています。単純に教育的なプレゼンテーションが優れています。
全部は読めなくていい
というわけで、数学書が難しい理由、読みにくい理由について分析してきました。解決方法も多少は提示できた気がします。
僕の結論としては、数学書は難しいものだと認めるしかありません。難しいことは必ずしも悪いことではなく、論理的に丁寧に書かれた結果難しいものであれば、慣れてしまえば親切な本と言えます(今回紹介したのは、どれも僕がお世話になった本です)。しかし、それは数学的議論に慣れた上で分野の全体像をある程度知っている人向けのもの。そういう本を初学者に勧めるのは、とても厳しいです。学問に王道なし、とは言いますが、先人の道を辿るだけでなく、歩きやすい道を開拓するのも大事な仕事ではないでしょうか。
数学書は難しいからこそ、冒頭から全部読むことは(初学者には)おすすめしません。挫折するのが目に見えています。
最初は読みやすい本を選ぶか、読みたくなる例や動機づけのある部分から読んでいくことをおすすめします。もしある数学書を学ぶ意義がわからないと感じたら、自分が意義のあると思う専門分野(数学以外でも良い)を学んでみて、そこでどういう数学が必要なのかを知った方が良いでしょう。
ほんの1行、1ページでも理解できることがあれば、それは大きな収穫です。こんなに分厚い本は全部読めない……と諦めることなく、自分なりに噛み砕いて、「ここだけはわかった!」と思えるポイントを積み重ねていくことが、数学書を読む能力につながっていきます。
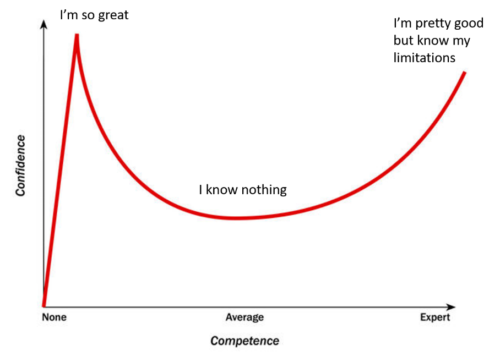
画像引用:Where Are You On The Dunning-Kruger Wiggle? – TRAININGPEAKS
「完全にわかった」を無理に目指さず、「読んだけど難しくて全然わからない」「ちょっとわかる」を目指してみてはいかがでしょうか。
木村すらいむ(@kimu3_slime)でした。ではでは。
東京大学出版会 (1966-03-31T00:00:01Z)
¥2,090
サイエンス社 (1990-01-01T00:00:01Z)
¥1,870
東京大学出版会 (2019-03-08T00:00:00.000Z)
¥2,750
共立出版 (1980-11-01T00:00:01Z)
¥5,390
世界標準MIT教科書 ストラング:線形代数イントロダクション
近代科学社 (2016-07-08T00:00:00.000Z)
¥4,400
こちらもおすすめ
厳密さ・証明が現代数学で要求されるのはなぜ? 近代数学の歴史をたどる
「自明、明らかである」に気をつけて、疑いながら数学書を読もう
数学の学びを深めるために必要なのは、「わからない」と言える力
なぜ教養数学として微積分学と線形代数学を学ぶのか ブルバキが現代数学に与えた影響