どうも、木村(@kimu3_slime)です。
大学で物理を学び始めると、初歩的な微積分や線形代数では足らない数学の知識が必要となってきます。
今回は、それらが学べる三井・山崎「物理数学」を紹介します。記事公開時点で、読み放題サービスKindle Unlimitedの対象となっているのでお得です。
どんな本か
三井・山崎「物理数学」は、物理で必要な数学(ベクトル解析、複素解析、フーリエ解析)を解説する教科書です。
著者いわく、これの内容は物理学を志す人にとっての「掛け算九九」のようなもの。一方で、それらの習熟は初心者にとって大変です。そのギャップを埋めるのがこの本と言えるでしょう。
大学1年次の物理の授業で必要とされる数学は、1年次の数学の講義、線形代数学と微積分学を超えているケースがあります。僕の記憶では、力学の講義で線積分・面積分が、電磁気学の講義でガウスの発散定理が登場して、戸惑って慌てて勉強しました。
本書は基本的に、定義とその導出、具体例、その計算方法、定義……という繰り返しを取って進んでいきます。
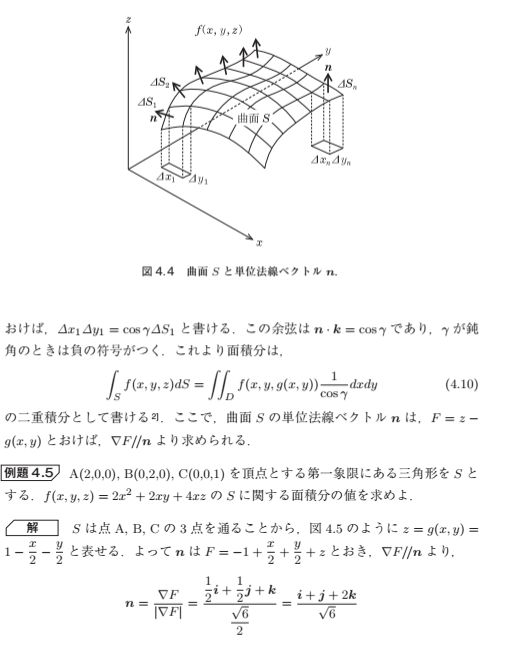
引用: 三井・山崎「物理数学」
全体を通して良いと思ったのは、定義の導出が詳しく、証明がしっかりついていること。単なる参考書ではなく、教科書という感じがします。
それでありながら一般論を展開しすぎず、必ず簡単な具体例を出して、その計算方法を見せてくれています。
目次
- 第I部 ベクトル解析
- 第1章 ベクトル
- 第2章 ベクトルの微分と積分
- 第3章 スカラー場とベクトル場
- 第4章 線積分と面積分
- 第5章 曲線座標
- 第II部 複素解析
- 第6章 複素数と複素平面
- 第7章 複素積分
- 第8章 極と留数、留数定理
- 第III部 フーリエ解析
- 第9章 周期関数のフーリエ展開
- 第10章 フーリエ変換
- 第11章 フーリエ変換の性質
- 第12章 フーリエ変換を用いた微分方程式の解法
気になる点
十分に話題は広く取られていると思いますが、掛け算九九レベルで習熟するには、やはり具体例や問題が不足しているように思います。
ベクトル解析、複素解析、フーリエ解析を広く扱った演習書としては「基礎数学7解析演習」が充実しています。ベクトル解析、複素解析を扱ったより厳密な教科書としては杉浦「解析入門 Ⅱ」が詳しいです。
複素解析に関しては、神保「複素関数入門」は同レベルの記述の親切さがありつつ、より広い話題を扱った教科書です。
フーリエ解析の偏微分方程式への応用としては、「偏微分方程式―科学者・技術者のための使い方と解き方」が具体的な計算が身につけやすくて良いと思います。
フーリエ解析の一般論として、やさしめの良い本を僕は知りません……。黒田「関数解析」は、ルベーグ積分の知識が要求されますが、フーリエ解析の一般論を詳しく扱っている教科書です。
やはり一気にこうした数学の教科書を読むのは大変です。まずは「物理数学」の枠組みを知り、その都度深く知りたくなった分野について教科書を買うのが良いでしょう。
僕は 三井・山崎「物理数学」を、Kindleの読み放題サービスKindle Unlimitedで読みました。登録してあれば無料なので、ぜひ試しに読んでみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
日本評論社 (2018-07-24T00:00:01Z)
¥2,640
東京大学出版会 (2019-03-08T00:00:00.000Z)
¥2,860
東京大学出版会 (1985-04-25T00:00:01Z)
¥3,740
岩波書店 (2003-12-12T00:00:01Z)
¥2,640
朝倉書店 (1996-12-01T00:00:01Z)
¥6,820
共立出版 (1980-11-01T00:00:01Z)
¥5,390
こちらもおすすめ
ベクトル値関数をベクトル場として描いてみよう:ヤコビ行列と線形近似
熱方程式の解き方:変数分離法、フーリエ級数展開(1次元、有界領域)