手頃な入門書「目からうろこの線形代数」レビュー

どうも、木村（@kimu3_slime）です。

線形代数を学んでみたいけれど、重い教科書に手を出す勇気はない……。

今回は、そんな方に読み放題サービスKindle Unlimitedの対象となっている「目からうろこの線形代数」を紹介します。

どんな本か
目次
気になる点
こちらもおすすめ

どんな本か

「目からうろこの線形代数」は、線形代数学をやさしく解説する本です。

やさしいというのは、2行2列、3行3列の行列をメインに計算していくからです。本書は、物理専攻の人と、農学を専攻する2人の著者によって作られていて、数学や物理を専門としない人がわかるレベルまで噛み砕く努力を感じます。

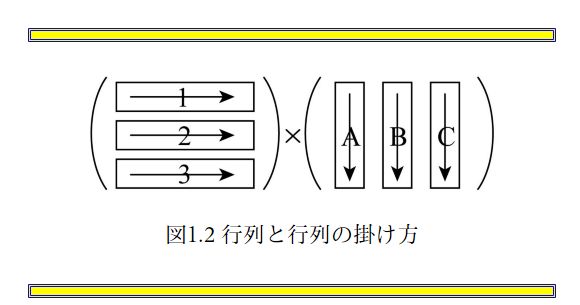
引用：目からうろこの線形代数 No.169

話はつるかめ算から始まり読み物のようですが、線形写像や線形空間と、線形代数らしい話題にもちゃんと踏み込んでいきます。

抽象的な話題も、それを何に使うか迷わせない工夫があると感じます。例えば、線形写像の話をしてすぐに固有値、対角化の話を軽く予感させている。また、固有値の話の導入に、人口変動の予測、マルコフ行列の話がされていて、学ぶ意義がわかりやすいです。

参考：なぜ線形代数を学ぶか：人々の移動予測とマルコフ過程

気になる点

表記法（ノーテーション）が気になる箇所があります。\(A \overrightarrow{X} = \overrightarrow{b} \)のように、同じ次元のベクトルなのに小文字と大文字が混同する。これは、太字を使わない（使えない）せいでしょう。また、索引がないのも不便です。

代わりに、本書はKindleに適応した可変レイアウトで、モバイルでも文字が小さくなることなく読みやすいです。本文を検索できるのも、固定レイアウトの教科書にはないメリットです。

また、完全に論理的な順序で話が進むわけではないのも気になります。例えば、固有値の話をする中で、m次元空間という言葉が登場しますが、その定義は後に示されます。もしわからない言葉があったら、先へ進むか別の教科書を当たる必要があるでしょう。

ほか、2次形式の話はあまりに短すぎて、話題として盛り込む意味がないのではないかと思います。2次形式について知りたいなら、例えば「線型代数入門」をあたると良いです。

線形代数の発展的な話題として、フーリエ変換の話を盛り込むのはチャレンジングで面白いのですが、「周期が2πの関数は～と書くことができます」から始まっており唐突です。例えば、「フーリエ変換の理論によると……」といった何が事実の担保となっているのかの補足が必要ではないでしょうか。

僕は線形代数の初心者向けの教科書として、「ストラング：線形代数イントロダクション」をおすすめしています。限りなくやさしく詳しい本だと思いますが、問題は、分厚いこと、またお値段がはることです。

「目からうろこの線形代数」は500円と格安。これほどの値段で、線形代数の話題がやさしく書かれた本を知りません。コスパが良すぎるので、他の数学分野でもぜひ出してほしいです。さらには、Kindleの読み放題サービスKindle Unlimitedに登録してあれば無料なので、ぜひ試しに読んでみてください。

木村すらいむ（@kimu3_slime）でした。ではでは。