大学数学を独学するための方法・考え方

どうも、木村（@kimu3_slime）です。

大学数学を独学したい。大学入試を終えて入学前の僕は、独学にチャレンジしてみましたが、うまくいきませんでした。

結果、大学に入り数学科へ進んでから、だんだんと大学数学の独学のやり方・考え方がわかってきました。そのポイントをかいつまんで紹介します。

自分なりのテーマを探そう
数学書の読み方を知る
アウトプットの場を作る
高校レベルの数学をおさえる

自分なりのテーマを探そう

まず、「大学数学」とは何か？どんな分野があるかをロードマップで確認しておきましょう。

大学数学のロードマップ～分野一覧と学ぶ順序

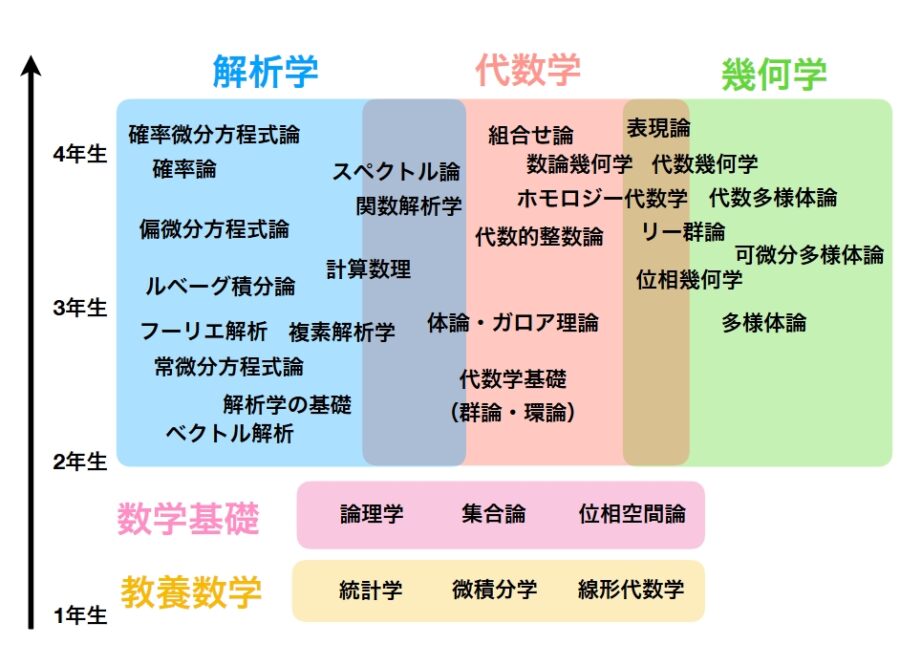
言葉の意味はわからなくて問題ありません。図書館で数学の棚へ行き、これらのキーワードの本をパラパラとめくってみましょう。中には興味を持てるものが見つかるかもしれません。

当サイトでも多くの本を紹介しています。本や映画から、これができたら楽しそうだな、カッコいいな、といったテーマを見つけてみてください。

参考：Kindle Unlimitedで読み放題、おすすめの数学本を紹介、「趣味の大学数学」おすすめ教科書・参考書・入門書

数学書の読み方を知る

僕が大学数学を学び始めようとしたときにつまづいたのが、大学数学の本の読み方です。

高校までの数学は、公式を覚えて計算できれば良い、という印象がありました。大学数学の本では、公式は「定理」と呼ばれ、その定理を「定義」から「証明」していくことに重点が置かれています。

参考：大学数学の教科書の読み方、最初に「定義・命題・証明」を知ろう

つまり、論理学の言葉で書かれた命題を読み解く能力が求められます。大学数学でどの分野を学ぶにせよ、まずはじめに論理学の本を読んでみると良いでしょう。

参考：論理学は大学数学のためだけでなく、教養として身につけたい

特に、集合と写像（関数）、論理の話は、教養数学の教科書でも最初に書かれていることが多いです。数学の「言葉」の約束を知らなければ、本は読み解きにくいでしょう。教科書の中身がわからないときは、出発点を確認してみてください。

参考：「AならばB」のよくある誤解から学ぶ、論理学入門（対偶、逆、否定、真偽表）、集合論のはじまり、全称命題と存在命題、論理記号を知ろう

アウトプットの場を作る

本をじろじろ眺めているだけでは、いくら時間をかけても数学は身につきません。

ノートとペンを用意し、本に書いてあることの計算を確かめたり、具体例を作ってみたりしてみましょう。本に書いてあることで「わからない」ことを発見し、自覚していくことが大事です。

参考：数学の学びを深めるために必要なのは、「わからない」と言える力

Twitterアカウントを作り、勉強記録をつけたり、わからないことをメモするのも良いでしょう。数学用アカウントを作っても良いですし、普通のアカウントでちょっと数学の話題をしてみたり。数学関係のアカウントをフォローし、交流する過程で耳学問ができます。数理科学関係の人を集めた、個人的に作ったリストを参考にしてみてください。（興味があれば、僕のアカウント@kimu3_slimeをフォローしてね）

何かしら数学関係の文章を、ネットにアップするのも勉強になります。情報を発信すれば、その話題に関心がある人が興味を持ってくれます。数学特化の情報共有サービスMathlog、TeXの使えるはてなブログはおすすめです。僕自身、「趣味の大学数学」で記事を書くこと自体が、数学の勉強になっています。

もし数学を学ぶ仲間、近い分野を学んでいる人がいたら、一緒に本を読む会、セミナー（ゼミ）・輪読会をすると良いでしょう。お互いに勉強したことを発表するのは、緊張するかもしれませんが、数学力を大きく伸ばすきっかけとなるでしょう。