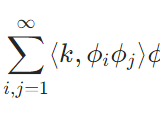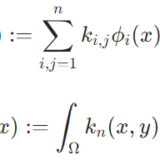有限ランク作用素とは、コンパクト作用素であることの証明

どうも、木村（@kimu3_slime）です。

今回は、有限ランク作用素とは、コンパクト作用素であることの証明を紹介します。

定義、例
コンパクト作用素であることの証明
こちらもおすすめ

定義、例

\(X,Y\)をノルム空間、\(F:X \to Y\)を有界線形作用素とします。\(F\)が有限ランク作用素（finite-rank operator）とは、像\(F(X)\)が有限次元の空間の部分集合となることです。有限階作用素、有限次元作用素とも。

\(F\)が線形写像なので、その像\(F(X)\)は線形空間となりますが、その次元\(\dim(F(X))\)を\(F\)のランクと呼びます。

例えば、\(N\)次の可逆行列\(A\)は有限ランク作用素です。実際、可逆であることは、像の次元が\(N\)であること、ランクが\(N\)であることと同値です。

（ゼロ作用素でない）有界線形汎関数\(F:X \to \mathbb{R}\)は、有限ランク作用素です。像は常に\(F(X) \subset \mathbb{R}\)となるので。

\(X=Y=L^2(\Omega)\)、\((k_{i,j}),c_{\ell}\)を係数として、\(F_n:X\to Y\)を\(u=\sum_{\ell=1}^\infty c_{\ell} \phi_{\ell}\)（\((\phi_\ell)\)は\(L^2\)の完全正規直交系）に対し\(F_n(u):=\sum_{i,j=1}^n k_{i,j}c_j \phi_i\)により定めると、\(F_n\)は有限ランク作用素です。

実際、\(F_n\)は線形作用素なので、その像\(F_n(X)\)は線形空間となります。\(F_n(X)\)の要素は\(\sum_{i,j=1}^n k_{i,j}c_j \phi_i\)と表されますが、\((\phi_\ell)\)は完全正規直交系なので、\((\phi_i)_{i=1}^n\)は線形独立で、\(\sum_{i,j=1}^n k_{i,j}c_j \phi_i\)はその線形結合で表せています。よって、\((\phi_i)_{i=1}^n\)は像の基底で、\(F_n(X)\)は\(n\)次元の部分空間、特に有限次元の部分集合であることが示せました。この例は、ヒルベルト・シュミット作用素の近似に使えます。

コンパクト作用素であることの証明

有限ランク作用素は、コンパクト作用素の一種です。つまり、有限作用素は必ずコンパクト作用素となります。

\(F:X\to Y\)を有限ランク作用素とし、\(A\subset X\)を有界な部分集合としましょう。有限ランク作用素の定義と、\(F(A)\subset F(X)\)から、\(F(A)\)は有限次元の空間の部分集合です。有限次元のノルム空間において、ノルムは同値で、次元が等しいならば同型です。したがって、\(F(A) \subset \mathbb{R}^N\)とできます。

\(F\)は有界作用素で、\(A\)は有界な集合なので、\(F(A)\)も有界です。なぜか。\(a\in A\)に対し\(\|a\|_X <R\)、\(u \in X\)に対し\(\|F(u)\|_Y \leq M \|u\|\)としましょう。このとき、\(\|F(a)\|\leq M\|a\| \leq MR\)となるので。

よって、\(\overline{F(A)}\)は\(\mathbb{R}^N\)の有界な閉集合です（上の横線は閉包）。ユークリッド空間において有界な閉集合はコンパクトなので（ハイネ・ボレルの定理）、\(\overline{F(A)}\)はコンパクトです。これで\(F\)がコンパクト作用素であることが示せました。

以上、有限ランク作用素とは、コンパクト作用素であることの証明を紹介してきました。

コンパクト作用素であることの証明や構成方法として、有限ランク作用素は扱いやすいですね。

木村すらいむ（@kimu3_slime）でした。ではでは。