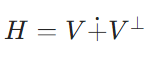コンパクト作用素のなす集合が有界作用素のなす空間B(X,Y)の部分空間となることの証明

どうも、木村（@kimu3_slime）です。

今回は、コンパクト作用素のなす集合\(B_c(X,Y)\)が有界作用素のなす空間\(B(X,Y)\)の部分空間となることの証明を紹介します。

前提の確認
証明
こちらもおすすめ

前提の確認

\(X,Y\)をノルム空間、\(F:X \to Y\)を線形作用素とします。\(F\)がコンパクトであるとは、\((u_n)\)を\(X\)の有界な点列とするとき、\((F(u_n))\)が\(Y\)において収束する部分列を持つことです。

\(B(X,Y)\)を有界な線形作用素のなすノルム空間とします。\(B_c(X,Y)\)をコンパクト作用素のなす集合とします（これは\(K(X,Y), \mathcal{K}(X,Y)\)と書かれることもあります）。

証明

コンパクト作用素ならば有界作用素であることは、別の記事で示しました。したがって、\(B_c(X,Y) \subset B(X,Y)\)です。

部分空間であることを示すためには、\(\lambda\)をスカラー、\(F_1,F_2 \in B_c(X,Y)\)として、\((\lambda F_1 +F_2) \in B_c(X,Y)\)を示せば良いです。

\((u_n)\)を\(X\)の有界な点列、「すべての\(n \in \mathbb{N}\)に対し\(\|u_n\|\leq M\)」を満たす\(M\)が存在するとしましょう。\(F_1\)がコンパクトなので、\((F_1(u_n)\)は収束する部分列を持ちます、それを\((F_1(u_{n_1(k)}))_k\)としましょう。

さらに、\((u_{n_1(k)})_k\)は\((u_n)\)の部分列なので、有界な点列です。したがって、\(F_2\)がコンパクトであることから、\((F_2(u_{n_1(k)}))\)は収束する部分列を持ちます。それを\((F_2(u_{n_2(k)}))_k\)としましょう。

後者の番号付けを組み合わせた点列\((F_1(u_{n_2(k)}))_k\)は、収束する点列\((F_1(u_{n_1(k)}))_k\)の部分列なので、収束します。

よって、収束する点列の定数倍、和は収束するので、\((\lambda F_1(u_{n_2(k)})+ F_2(u_{n_2(k)}))_k\)は収束します。関数の和の定義から、\((\lambda F_1+F_2)(u_{n_2(k)})= \lambda F_1(u_{n_2(k)})+ F_2(u_{n_2(k)})\)なので、\(\lambda F_1+F_2 \)がコンパクトであること、\((\lambda F_1+F_2) \in B_c(X,Y)\)が示せました。

つまり、コンパクト作用素の定数倍、コンパクト作用素同士の和はコンパクト作用素です。

以上、コンパクト作用素のなす集合\(B_c(X,Y)\)が有界作用素のなす空間\(B(X,Y)\)の部分空間となることの証明を紹介してきました。

さらに\(Y\)が完備ならば、\(B_c(X,Y)\)は閉部分空間、バナッハ空間となることが示せます。これについては別記事にて。

木村すらいむ（@kimu3_slime）でした。ではでは。