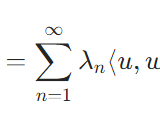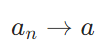どうも、木村(@kimu3_slime)です。
今回は、ヒルベルト空間の直交補空間が閉部分空間であることの証明を紹介します。
導入、定義
\(H\)をヒルベルト空間(完備な内積空間)、\(V \subset H\)を部分集合(必ずしも部分空間でなくて良い)とします。
\[V^{\perp}:= \{u \in H \mid すべてのv \in V に対し \langle u,v \rangle_H =0\}\]
これを\(V\)の直交補空間(orthogonal complement)と呼びます。
\(V^{\perp}\)は閉部分空間(閉集合であって、部分空間でもある)になります。
完備な距離空間の閉集合は完備であることが知られているので、\(V^{\perp}\)は完備でもあります。
一般に、有限次元の空間においては、部分空間はすべて閉集合になります。したがって、閉かどうかは気にしなくて良いでしょう。
しかし、無限次元の空間において、すべての部分空間が閉集合であるとは限りません。
例えば、2乗可積分関数のなす\(H=L^2\)において、連続関数のなす空間\(C^0\)は部分空間です。しかし、\(L^2\)ノルムで完備でないことを示す例のように、\(C^0\)の関数列で\(C^0\)の関数に収束しないものがあります。したがって、\(C^0\)は閉集合でなく、部分空間ではありません。
しかし、\(V^{\perp}\)は必ず閉部分空間となります。関数列の収束・極限を考えるときに便利な対象です。
証明
では、
\[V^{\perp}:= \{u \in H \mid すべてのv \in V に対し \langle u,v \rangle_H =0\}\]
が\(H\)の閉部分空間であることを証明しましょう。
部分空間であること
\(u,w \in V^{\perp}\)、\(\lambda\)をスカラーとします。内積の線形性から、すべての\(v \in V\)に対し、
\[\begin{aligned} &\langle \lambda u+w ,v \rangle_H \\ &= \lambda \langle u,v \rangle_H+\langle w ,v \rangle_H\\ &= 0 \end{aligned}\]
となるので(内積の第一成分に関する連続性)、\((\lambda u +v) \in V^{\perp }\)です。よって、\( V^{\perp}\)は部分空間です。
閉集合であること
\((u_n)_n\)を\(V^{\perp}\)の点列とし、\(\lim_{n \to \infty} \|u_n -u\|_H =0\)を満たす\(u\in H\)があると仮定し、\(u \in V^{\perp}\)であることを示しましょう。
\[\begin{aligned} &|\langle u,v\rangle_H-\langle u_n,v\rangle_H | \\ &= |\langle u-u_n ,v \rangle_H| \\ &\leq \|u-u_n\|_H \|v\|_H \\ & \to 0 \quad (n \to \infty)\end{aligned}\]
なので、\(u_n \in V^{\perp}\)から\(\langle u,v\rangle_H = \lim_{n\to \infty} \langle u_n,v\rangle_H =0\)です。つまり、\(u \in V^{\perp}\)で、\(V^{\perp}\)が閉集合であることが示せました。
基本的な性質
ここでは証明しませんが、いくつか基本的な性質を述べておきましょう。
- \(V\)が部分空間ならば、\(V\cap V^{\perp}=\{0\}\)
- \(V\)が部分空間ならば、\(V \subset (V^{\perp})^{\perp}\)
- \(V\)が閉部分空間ならば、\(V = (V^{\perp})^{\perp}\)
- \(V\)が閉部分空間ならば、\(H = V \dot{+} V^{\perp}\)(直和分解ができる)
以上、ヒルベルト空間の直交補空間が閉部分空間であることの証明を紹介してきました。
これは例えば、コンパクトな対称作用素の固有値の議論で応用されています。
木村すらいむ(@kimu3_slime)でした。ではでは。
Evans, Lawrence C.(著)
¥16,299 (2022-08-19時点)