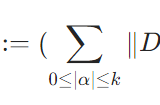弱形式、弱解とは：ポアソン方程式を例に

どうも、木村（@kimu3_slime）です。

今回は、弱形式、弱解とは何か、ポアソン方程式を例に紹介します。

ポアソン方程式とは
弱形式の導出、弱解の定義
弱解の性質
こちらもおすすめ

ポアソン方程式とは

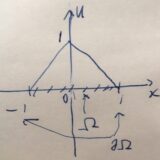
\(\Omega \subset \mathbb{R}^N\)を有界な開集合、\(\partial \Omega\)をその境界、\(f\)を\(\Omega\)上の連続関数とします。

\[-\Delta u (x)=f(x) \quad (x \in \Omega) \]

\[ u (x)=0 \quad (x \in \partial\Omega) \]

この方程式をポアソン方程式（Poisson’s equation）と呼び、これを満たす\(u \in C^2(\Omega) \cap C^0(\overline{\Omega})\)をその解と呼びます。

\(\Delta u =\frac{\partial^2 u}{\partial x_1^2}+\cdots +\frac{\partial^2 u}{\partial x_N^2}\)はラプラシアンと呼ばれ、2回微分の和です。

境界での値は0という条件が課してありますが、それはディリクレ境界条件と呼ばれるものです。

ポアソン方程式は、重力や電磁気のポテンシャル、また温度や化学物質の濃度を表す方程式として応用されています。特に\(f=0\)のケースは、ラプラス方程式（Laplace’s equation）と呼ばれています。ともに楕円型の偏微分方程式に分類されるものです。

全空間におけるポアソン方程式は基本解、有界集合においてはグリーン関数による解の表示式が知られ、解の性質がよく知られています。

弱形式の導出、弱解の定義

今回は、このポアソン方程式を、強い意味で微分可能とは限らない関数に対して一般化してみましょう。

弱微分の定義と同様に、テスト関数\(\phi \in C_c ^\infty (\Omega)\)を用いて、方程式を変形していきます。方程式の両辺に\(\phi\)をかけて\(\Omega\)上で積分すると、

\[-\int_\Omega (\Delta u (x)) \phi (x)dx = \int_\Omega f(x)\phi (x)dx \]

です。左辺を部分積分すると、テスト関数の効果によって境界での項は消え、

\[\begin{aligned} &-\int_\Omega (\Delta u (x)) \phi (x)dx \\ &= -\int_\Omega (\sum_{k=1}^N \frac{\partial^2 u}{\partial x_k ^2}) \phi dx \\ &= -\sum_{k=1}^N\int_\Omega \frac{\partial^2 u}{\partial x_k ^2} \phi dx \\ &= \sum_{k=1}^N\int_\Omega \frac{\partial u}{\partial x_k } \frac{\partial \phi}{\partial x_k} dx \\ &= \int_\Omega \langle \nabla u, \nabla \phi \rangle dx\end{aligned}\]

となります。\(\nabla u =(\frac{\partial u}{\partial x_1},\dots,\frac{\partial u}{\partial x_N})\)は勾配ベクトル、\(\langle \cdot,\cdot \rangle\)はユークリッド内積です。

つまり、従来の意味でのポアソン方程式は、すべての\(\phi \in C_c ^\infty (\Omega)\)に対し、

\[\int_\Omega \langle \nabla u, \nabla \phi \rangle dx = \int_\Omega f(x)\phi (x)dx \]

を満たします。この形の方程式（積分方程式）は、\(u,f\)が強い意味で微分可能や連続でなくても定義できますね。

そこで、\(L^p\)空間やソボレフ空間の関数を用いて、弱い形で定式化しましょう。

右辺の積分による内積が定義できるよう、\(f \in L^2 (\Omega)\)とします。\(u\)は1回弱微分可能であり、ディリクレ境界条件を課しているので境界で0、\(u \in H_0 ^1 (\Omega)\)とします。テスト関数は少し範囲を広げ、完備化した\(H_0 ^1 (\Omega)\)を考えます。

つまり問題は、与えられた\(f \in L^2\)を与えられたものとし、すべての\(\phi \in H_0 ^1 (\Omega)\)に対し、

\[\int_\Omega \langle \nabla u, \nabla \phi \rangle dx = \int_\Omega f(x)\phi (x)dx \]

を満たすような\(u \in H_0^1 (\Omega)\)を求めよ、と定式化することができました。これをポアソン方程式の弱形式（weak form）といい、この問題の解を弱解（weak solution）、一般化された解と呼びます。

これに対して、強い意味で微分可能な関数が満たす従来のポアソン方程式の問題は強形式（strong form）と呼ばれ、その解は強解（strong solution）、古典解（classical solution）と呼ばれます。

強微分可能ならば弱微分可能なので、ポアソン方程式の強解は必ず弱解になります。こうした意味で、弱形式は一般化されたポアソン方程式、弱解は一般化された解になっているわけです。

弱解の性質

弱解を調べるためには、まずそれが一意に存在するかどうかを知る必要がありますね。

実際、ラプラス方程式の弱解は、一意に存在することが知られています。そこで用いるのが、関数解析の定理、リースの表現定理です。

リースの表現定理（Riesz representation theorem）

\(H\)を完備な内積空間（ヒルベルト空間）とする。

どんな有界線形汎関数\(\ell \in H^{*}\)に対しても、次の条件を満たす\(x_\ell \in H\)が一意に存在する。

すべての\(y \in H\)に対し、\(\ell (y)= \langle x_{\ell},y \rangle \)

この定理の仮定において、用いる関数空間が完備であることが必要になります。だからルベーグ積分論やソボレフ空間の議論が必要になるわけです。

さらに、\(-\Delta\)を関数に対する作用素として見ると良い性質を持ち、可算無限個の固有関数で、\(L^2(\Omega)\)の完全正規直交基底であるようなものが存在することが示せます。これは解の近似、ガラーキン法の基礎です。

また、弱解の存在と一意性によれば、解は\(u \in H_0^1 (\Omega)\)であることしかわかりません。\(f\)の連続性・なめらかさ次第で、解\(u\)もなめらかになる可能性があります。

実際は、ラプラス方程式では、弱解はなめらかな関数になります（これはラプラス方程式の著しい性質で、明らかなものではありません）。例えば、\(f \in C^\infty\)ならば、\(u \in C^\infty\)になります。弱解のなめらかさを示すには、ノルムを不等式評価する必要があり、それはレギュラリティ（regularity）問題と呼ばれています。

弱解の考え方は、今回のようなラプラス方程式だけでなく、それを一般化した方程式や、他の偏微分方程式に対しても利用できるものです。

例えば、\(-\Delta\)を一般化した楕円形作用素に対しても弱解の問題が考えられます。

その問題の解の一意性は、リースの表現定理を応用したラックス・ミルグラムの定理を用います。

時間変化するような偏微分方程式において、解の存在と一意性（やその性質）がわかれば、解の時間変化：力学系の議論をすることができますね。

弱解やそのなめらかさに関して有名な問題としては、100万ドルの懸賞金がかけられたミレニアム問題のうちのひとつ、ナビエ–ストークス方程式の解の存在と滑らかさが有名ですね。

これも弱解やそのレギュラリティ（なめらかさ）を調べる問題といえ、部分的には解決されていますが、全体としては未解決問題であるようです。

以上、弱形式、弱解とは何か、ポアソン方程式を例に紹介してきました。

ポアソン方程式そのものは、比較的性質がよく知られており、問題を一般化したり弱解を導入する必然性を感じにくいかもしれません。例えば波動を表すバーガース方程式では、連続でなくなる解：衝撃波解が存在します。

しかし、たとえ解が実際には連続になるとしても、弱解の理論は役立ちます。解の表示式を得る＝具体的に解くことにこだわらず、存在と一意性を示す＝抽象的に解くことによって、問題を一般的に解きやすく分割しているのです。その解析のツールとして、関数解析が役に立ちます。

今回の話が、偏微分方程式や関数解析、ルベーグ積分を学ぶモチベーションのひとつになれば嬉しいです。

木村すらいむ（@kimu3_slime）でした。ではでは。