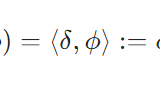どうも、木村(@kimu3_slime)です。
今回は、相対位相、部分集合における開集合・閉集合とは何か、ユークリッド空間の位相を例に紹介します。
導入と定義
例えばテスト関数を定義するときに、関数\(\phi\)の台
\[\mathrm{supp }\, \phi:= \overline {\{x\in \Omega \mid \phi(x) \neq 0\}} \]
を考えます。ここで\(\Omega \)を\(\subset \mathbb{R}^N\)の開集合で、台の定義では、\(\Omega\)における閉包を考えています。
この「部分集合における閉包(開集合・閉集合)」という表現について、具体例を踏まえて解説していきましょう。
\((X,\mathcal{O})\)を位相空間とし、\(A\)を\(X\)の部分集合としましょう。
\(A\)の部分集合族を\(\mathcal{O}_A:=\{ O \cap A \mid O \in \mathcal{O} \}\)と定めます。すると、\((A, \mathcal{O}_A)\)はそれ自身が位相空間の定義を満たします。
そこで、\((A, \mathcal{O}_A)\)を\((X,\mathcal{O})\)の部分位相空間(subspace)と呼びます。また、\(A\)の開集合系\(\mathcal{O}_A\)を相対位相(relative topology)、部分空間位相、誘導される位相などと呼びます。
特に、\(\mathcal{O}_A\)の要素を\(A\)における開集合と呼びます。簡単に言えば、全体\(X\)における開集合\(O\)と\(A\)の共通部分として表せるのが、\(A\)の開集合です。
\(A\)における開集合の\(A\)における補集合を、\(A\)における閉集合と呼びます。全体\(X\)における閉集合\(C\)と\(A\)の共通部分として表せるのが、\(A\)の閉集合とも言えます。
相対位相を考えるときは、どこにおける開集合(閉集合)なのか意識することが大事です。
例
1次元ユークリッド空間\((\mathbb{R},\mathcal{O})\)の簡単な例を挙げましょう。
\(A=(-1,1)\)という開区間を考えます。\(A\)における開集合、閉集合の例を考えてみましょう。
\(B_1=(-\frac{1}{2},\frac{1}{2})\)は、\(\mathbb{R}\)における開集合です。また、\(A\)の部分集合でもあるので、\(B_1 = B_1 \cap A\)、\(B_1 \in \mathcal{O}\)となるので、\(B_1\)は\(A\)における開集合でもあります(\(B_1 \in \mathcal{O}_A\))
一般に、全体\(X\)における開集合であって、かつ\(A\)の部分集合でもある集合は、\(A\)の開集合です。
閉集合についても同様です。\(B_2=[-\frac{1}{2},\frac{1}{2}]\)は、\(\mathbb{R}\)における閉集合であり、かつ\(A\)における閉集合でもあります。
ここまでの例では、開集合・閉集合が一致していましたが、一般にはそうとは限りません。
\(B_3 = (-1,1)\)が\(A\)における閉集合であるか考えてみましょう。
\(B_3\)は、\(\mathbb{R}\)においては閉集合ではありません。\(\mathbb{R}\)における補集合は、\(\mathbb{R} \setminus B_3 =(-\infty , -1]\cup [1,\infty)\)であり、\(-1,1\)が内点ではなく、補集合が開集合ではないからです。
一方で、\(B_3 = (-1,1)\)は\(A\)における閉集合です。\(\mathbb{R}\)の閉集合\([-1,1]\)を使って、\(B_3 = [-1,1] \cap A\)と表せるので。\(B_3\)の\(A\)における補集合は、\(A \setminus B_3 = \varnothing\)で、補集合が\(A\)における開集合なので、\(A\)における閉集合とも言えます。
位相空間の扱いに慣れていないと、「\((-1,1)\)は常に開集合であり、閉集合でない」と考えてしまうかもしれません。「\((-1,1)\)は\(\mathbb{R}\)の閉集合でないが、\((-1,1)\)における閉集合ではある」わけですね。
一般に、部分位相空間\((A, \mathcal{O}_A)\)において、\(A\)自身は開集合であり、かつ閉集合でもあります。考えている全体空間が開集合かつ閉集合になることが、そもそも位相空間の定義のひとつなので。
例えば、全体においては開集合でないが、相対位相では開集合となる例を挙げられるでしょうか?
\([-1,1]\)がそうですね。これは\(\mathbb{R}\)にいては開集合ではありませんが、\([-1,1]\)においては開集合です。例えば、\([-1,1]=(-2,2) \cap [-1,1]\)、\((-2,2) \in \mathcal{O}\)となるので。
冒頭の例に戻り、
\[ \phi(x)= \left\{ \begin{array}{lr} e^{-\frac{1}{1-x^2}} && (|x|<1) \\ 0 && (|x| \geq 1) \end{array} \right. \]
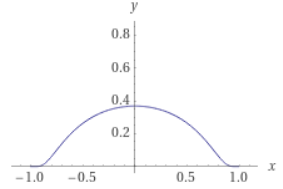
というテスト関数の\(\Omega=(-1,1)\)における台
\[\mathrm{supp }\, \phi:= \overline {\{x\in (-1,1) \mid \phi(x) \neq 0\}} \]
を求めてみましょう。ここでバー(閉包)は、\(\Omega\)における閉包、中身の集合を含む最小の\(\Omega\)における閉包を表しています。
まず、0でない値を取る定義域は
\[{\{x\in \Omega \mid \phi(x) \neq 0\}}=(-1,1) \]
です。そして、\((-1,1)\)は、\((-1,1)\)を含み、それ自身が\((-1,1)\)の閉集合なので、
\[\mathrm{supp }\, \phi= \overline {\{x\in (-1,1) \mid \phi(x) \neq 0\}} \\ \overline{(-1,1)} =(-1,1)\]
と求めることができました。閉包を取ったからといって、端点を含むとは限らないのです。
もし\(\mathbb{R}\)における閉包を考えると、\(\mathrm{supp }\, \phi=[-1,1]\)ですが、これは議論しようとしている定義域\(\Omega =(-1,1)\)をはみ出してしまっていて困りますね。このような事態を避けるために、\(\Omega\)における閉包を台の定義では考えたわけです。
以上、相対位相、部分集合における開集合・閉集合とは何か、ユークリッド空間の位相を例にを紹介してきました。
開集合・閉集合という位相的な用語はさまざまな分野で使われていますが、「どこかの部分集合における」という但し書きがついているときは、部分位相空間、相対位相の話を思い出してみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
Evans, Lawrence C.(著)
¥16,299 (2022-08-19時点)