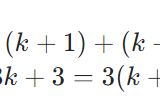どうも、木村(@kimu3_slime)です。
今回は、連続する3つの偶数の和が6の倍数となることの証明、一般化を紹介します。
説明と予想
偶数とは、\(2=2\times 0\)、\(4=2\times 2\)、\(6=2\times 3\)のような、2の倍数のことでした。
連続する3つの偶数とは、「2、4、6」や「6、8、10」のように、そのうち最も小さな偶数から2ずつ増やした数たちのことです。隣り合う3つの偶数とも。例えば、「2、6、10」は3つの偶数ではありますが、連続した3つの偶数ではありません。
「2、4、6」や「6、8、10」の和とは、それらを足し合わせたもののことです。計算して試してみましょう。
\[2+4+6= 12 =6\times 2\]
\[6+8+10=24 =6 \times 4\]
と、確かに6の倍数となっていますね。
証明
では、一般的な形で証明していきましょう。
連続する3つの偶数は、何かしらの整数\(k\)によって、\(2k,2k+2,2k+4\)と表せます。それらの和は、
\[2k+(2k+2)+(2k+4)\\ =6k+6\\ = 6(k +1)\]
となります。\(k+1\)は整数なので、\(6(k+1)\)は6の倍数です。よって、連続する3つの偶数の和は、6の倍数となることが示せました。
説明の方法は、次のようなものでも実質的に同じです。
例えば、途中の計算の\(6k+6\)に注目します。\(6k\)は6の倍数で、\(6\)は6の倍数です。6の倍数の和は6の倍数なので、\(6k+6\)は6の倍数です。
連続する3つの偶数の表し方を、次のようにも変えられます。\(2k-2,2k,2k+2\)と。それらの和は、
\[(2k-3)+(2k)+(2k+2)\\ = 6k\]
です。これは6の倍数です。シンプルですね。
\[2k+(2k+2)+(2k+4)\\ =6k+6\\ = 6(k +1)\]
という計算を別の視点で眺めると、これは真ん中の偶数の3倍となっています。
つまり、「連続する3つの偶数の和は、真ん中の偶数の3倍となる」とも言えるわけですね。
一般化
この問題を一般化すると、「連続する\(n\)個の偶数の和は\(n\)の倍数となる」と言えます。
総和の記号(シグマ記号)を使って和を表し、和の公式\(\sum_{\ell=1}^n \ell = \frac{1}{2}n(n+1)\)によって計算しましょう。
連続する\(n\)個の奇数の和は、
\[(2k+2)+\cdots+(2k+2n)\\= \sum_{\ell =1}^{n} (2k+2\ell )\\ = 2nk+2 \cdot \frac{1}{2}n(n+1)\\=n(2k+n+1)\]
となります。\(2k+n+1\)は整数なので、\(n(2k+n+1)\)は\(n\)の倍数です。よって、連続する\(n\)個の奇数の和は、\(n\)の倍数であることが示せました。
例えば、
- 連続する4つの偶数の和は4の倍数
- 連続する5つの偶数の和は5の倍数
と言えます。
途中の計算を見ると、\(n\)が奇数のときは、\(2k+n+1\)が偶数となり、結果として連続する偶数の和が\(2n\)の倍数になると言えます。
これの特殊なケース、\(n=3\)のときが6の倍数と言えたわけですね。
\(n\)が偶数のときは、和が\(2n\)の倍数になるとは限りません。例えば、\(n=4\)のとき、\(2,4,6,8\)について考えると、
\[2+4+6+8=20 = 4\times 5\]
で、\(4\)の倍数ではありますが、\(8\)の倍数ではありません。
以上、連続する3つの偶数の和が6の倍数となることの証明、一般化を紹介してきました。
連続する3つの整数、連続する3つの奇数と合わせて、整数に関する簡単な証明問題としてぜひ扱えるようになっておきたいですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Elementary Geometry for College Students 5th (Fifth) Edition byAlexander
¥13,970 (中古品)