どうも、木村(@kimu3_slime)です。
今回は、各種の四角形の定義と分類、性質についてまとめました。
四角形の分類と定義
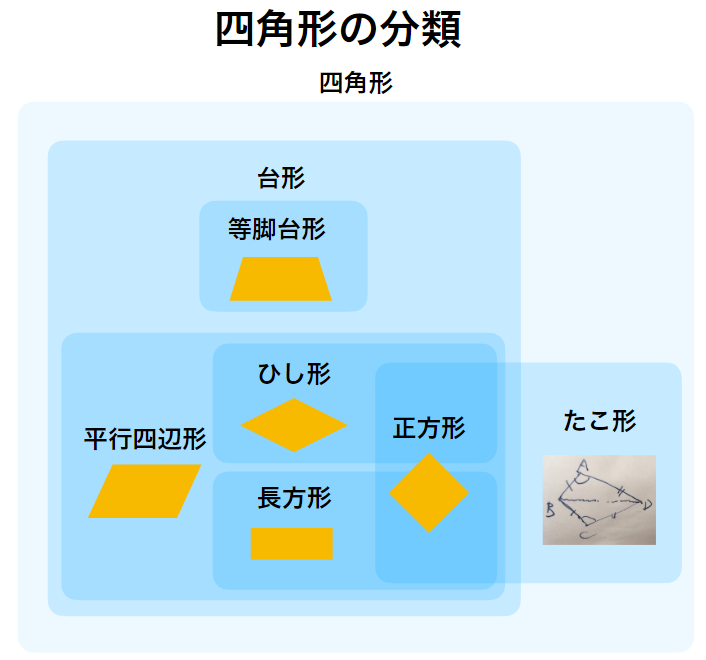
四角形の定義
- 四角形(quadrilateral):端点でしか交わらないような4つの線分によってできる図形。辺によって囲まれる内側(有界領域)も四角形と呼ぶことがある。
- 台形(trapezoid):2つ以上の平行な辺を持つ四角形。
- 等脚台形(isosceles trapezoid):ちょうど2つの平行な辺を持ち、平行でない2つの辺の長さが等しい四角形。
- 平行四辺形(parallelogram):向かい合う2組の辺が平行な四角形。
- ひし形(rhombus):4つの辺の長さが等しい四角形。
- 長方形(rectangle):向かい合う2組の辺が平行で、隣り合う辺が直交する四角形。
- 正方形(square):4つの辺の長さが等しく、隣り合う辺が直交する四角形。
- たこ形(kite):隣り合う2組の辺の長さが等しい四角形。
ここで述べた定義以外の方法でも、実質的に同じ図形を定義することはできます。つまり、この定義は唯一の定義ではなく、さまざまな流儀がありえるわけです。
例えば、「平行で長さの等しい2つの辺を持つ四角形」を平行四辺形の定義とし、「向かい合う2組の辺が平行」を性質として導くこともできます。
正方形は長方形か
ネットではしばしば「正方形は長方形か?」という問題が話題になります。
その答えは定義次第です。2種類の定義をはっきりさせましょう。
- 広義の長方形:向かい合う2つ(以上)の辺の長さが等しい四角形
- 狭義の長方形:向かい合う(ちょうど)2つの辺の長さが等しい四角形
正方形(4つの辺の長さが等しい四角形)は、広義の長方形の一種です。なぜなら、4つの辺の長さが等しいならば、その一部分、2つの辺の長さも等しいからです。
一方、正方形は狭義の長方形ではありません。なぜなら、正方形は4つの辺の長さが等しく、ちょうど2つの辺の長さが等しいわけではないからです。
小学校のテストでは、しばしば狭義の長方形を前提とした問題が出題されるようです。例えば、正方形はひし形ではない、といった排他的な分類をすることがあります。
最初に述べた定義では、排他的な分類をせず、基本的には広義の定義を採用しました。つまり、正方形は長方形の一種とした分類です。その包含関係を示したのが上の図でした。
狭義の定義では見た目による区別はつきやすいですが、論理的な定義が複雑になります(限定が必要になる)。広義の定義のほうが、各種の四角形の相互関係がわかりやすいです。また、「自然数は整数(の一種)である」といった数学の標準的な考え方と一貫性があります。
四角形の分類
上で述べたように定義すると、正方形は長方形の一種になります。すなわち、すべての正方形は長方形です(長方形でもある)。
これを集合の包含関係を使って
\[\{正方形\}\subset \{長方形\}\]
と表すことにしましょう。正方形全体の集合は、長方形全体の集合の部分集合と読みます。他の包含関係は、次のように表せます。
\[\{正方形\}\subset \{長方形\}\subset \{平行四辺形\}\]
\[\{正方形\}\subset \{ひし形\}\subset \{平行四辺形\}\]
\[ \{平行四辺形\} \subset\{台形\} \subset\{四角形\}\]
\[ \{等脚台形\} \subset\{台形\} \]
\[ \{正方形\} \subset\{たこ形\}\]
さらにこの包含関係は、真部分集合でもあります。例えば、長方形であるが正方形でないような例が存在します。
集合として等しくないこと、逆向きの包含関係が成り立たないような例を図示してみてはいかがでしょうか。
今回は分類に登場させませんでしたが、台形ではないが四角形である典型として、180度を超える内角を持つ四角形:凹四角形があります。ブーメランのような形がわかりやすいでしょう。
台形では、すべての内角は180度未満となり、頂点同士を結ぶ線分(対角線)は四角形の内側にある:凸四角形となります。小中学校では、四角形と言えば凸四角形を扱うことが多いでしょう。
四角形とは端点でしか交わらないような4つの線分によってできる図形でしたが、端点でしか交わらない有限個の線分によってできる図形は多角形(polygon)と呼ばれます。三角形や四角形は、多角形の一種です。
四角形の性質
以上で紹介してきた四角形の分類ごとの性質を、「Elementary Geometry for College Students 」を参考に表としてまとめます。
| 台形 | 等脚台形 | 平行四辺形 | |
| 長さの等しい辺 | 一般にはない | 1組の脚(定義) | 向かい合う2組の辺 |
| 平行な辺 | 1組の向かい合う辺(定義) | 1組の向かい合う辺(定義) | 2組の向かい合う辺(定義) |
| 直交する辺 | 一般にはない | 一般にはない | 一般にはない |
| 大きさの等しい角 | 一般にはない | 2組の底角 | 向かい合う2組の角 |
| 対角線 | 特になし | 長さが等しい | お互いを二等分する |
| 面積 | \(\frac{1}{2}(a+b)h\) | \(\frac{1}{2}(a+b)h\) | \(ah\) |
| ひし形 | 長方形 | 正方形 | |
| 長さの等しい辺 | 4つの辺(定義) | 2組の向かい合う辺(定義) | 4つの辺(定義) |
| 平行な辺 | 2組の向かい合う辺 | 2組の向かい合う辺 | 2組の向かい合う辺 |
| 直交する辺 | 一般にはない | 隣り合う辺(定義) | 隣り合う辺(定義) |
| 大きさの等しい角 | 向かい合う2組の角 | 4つの角 | 4つの角 |
| 対角線 | 直交する。お互いを二等分する。内角を二等分する。 | 長さが等しい。お互いを二等分する。 | 長さが等しい。直交する。お互いを二等分する。内角を二等分する。 |
| 面積 | \(\frac{1}{2}d_1d_2\) | \(ab\) | \(ab\) |
| たこ形 | |
| 長さの等しい辺 | 隣り合う2組の辺(定義) |
| 平行な辺 | 一般にはない |
| 直交する辺 | 一般にはない |
| 大きさの等しい角 | 1組以上の向かい合う角 |
| 対角線 | 直交する。一方が他方を二等分する。一方は2つの内角を二等分する。 |
| 面積 | \(\frac{1}{2}d_1d_2\) |
以上、四角形の定義と分類、性質をまとめてきました。
この記事が各種の四角形の相互関係を理解するきっかけとなれば嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
Elementary Geometry for College Students 5th (Fifth) Edition byAlexander
¥13,970 (中古品)
こちらもおすすめ
平行で長さの等しい2つの辺を持つ四角形は平行四辺形であることの証明
たこ形四角形の定義、大きさの等しい向かい合う角があることの証明