どうも、木村(@kimu3_slime)です。
僕はこのサイトで、中学高校大学の数学のロードマップを公開しています。たくさんの内容が書いてあるように見えますが、「こんなに学ばなくてはいけないの?」と怯えなくて良いという話をしていきます。
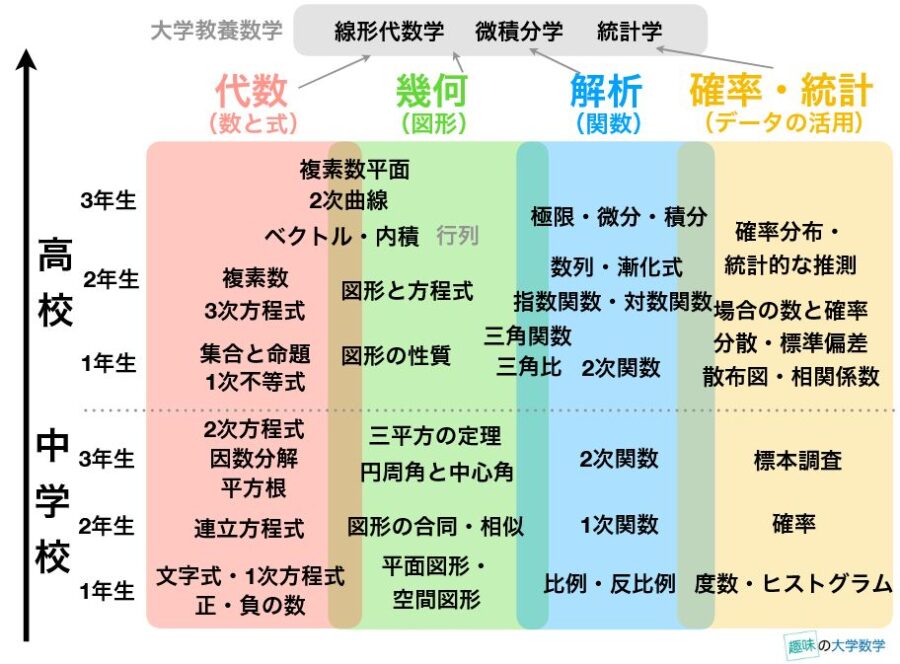
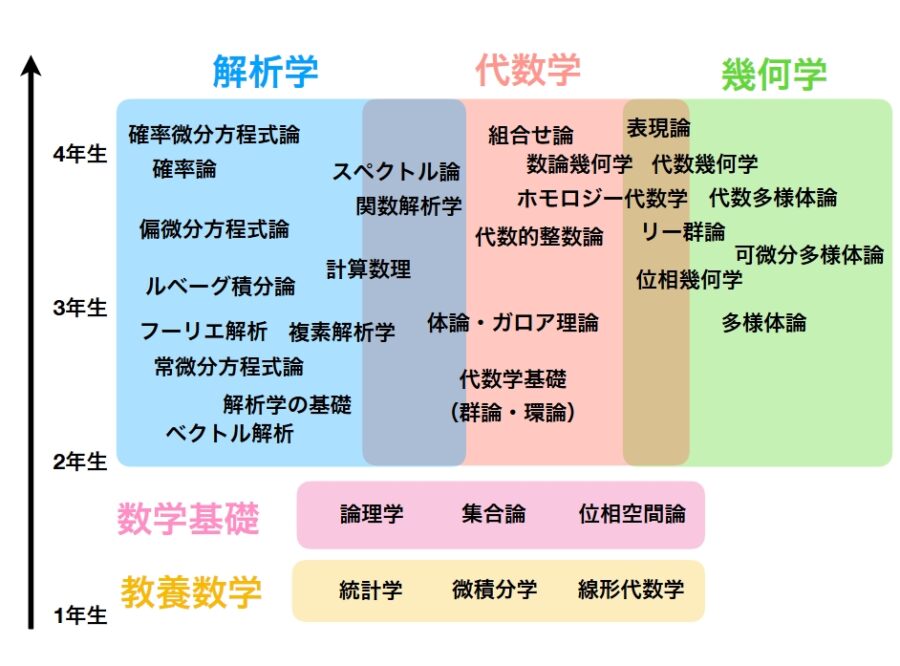
- 小学校:2,3桁程度の自然数・分数・整数の四則演算
- 中学校:初等代数(1・2次の多項式、方程式・平方根・不等式、座標平面・関数、面積、ピタゴラスの定理)
- 高校:初等関数(指数・対数・三角関数)と微積分
- 高校:ベクトルと行列
数学は1回では理解できない
数学を学ぶときに大事な心構えのひとつが、「1回で理解できるとは思わない」ことです。
自転車の乗り方や漢字の書き方を学ぶときに、1回では身につけられませんでしたよね? (できた人は相当賢いと思います) それと同じように、数学も同じ内容を何度も繰り返し練習しなければ、身につけられないのが普通です。
1回で身につけられなかったからといって、「自分には才能がない」と思わないようにしましょう。人間は一度きりのインプットで完全に学習できる機械ではないし、類まれなる天才ではないのが普通です。
僕が考える現代に生きる数学の天才のひとりとして、テレンス・タオがいます。彼は9歳にして大学に飛び入学し、数学の中でも圧倒的に幅広い分野の知識を身に着けながら研究を残し、数学の「ノーベル賞」ことフィールズ賞を受賞しています。
彼の頭の良いことはもちろんでしょうが、だからといってきっと一度ですべての数学を身に着けたわけではないでしょう。「幼い頃から難しい問題を次々と解くことで、思考が磨かれていった」と語る通り、長い時間をかけて数学に向き合ってきたからこそ、結果として優れた能力を発揮しているのだと思います。実際、彼のブログでもそのような言葉が残されています。
In short, there is no royal road to mathematics; to get to the “post-rigorous” stage in which your intuition matches well with what one can establish rigorously, one has to first invest real effort in learning and relearning the field, learning the strengths and weaknesses of tools, learning what else is going on in mathematics, learning how to solve problems rigorously, and answering lots of dumb questions, and so forth. This all requires hard work.
要するに、数学に王道はなく、自分の直感と厳密に確立できるものがうまくマッチする「ポスト厳密」の段階に行くには、まず、その分野の学習と学び直し、道具の長所と短所を学び、数学で他に何が起こっているかを知り、問題を厳密に解く方法を学び、たくさんの馬鹿な質問に答えるなど、本当の努力をしなければならないのです。これにはすべてハードワークが必要です。
僕もあなたもきっと、テレンス・タオではないし、ガウスやラマヌジャンでもありません。しかし彼らは無条件に数学の天才であったわけではなく(もちろん適性はあったでしょうが)、時間と思考を数学に注ぎ込んだからこそ得たものがあったわけです。
才能がある人ですら数学を理解するのに時間をかけているのですから、凡人たる我々は尚更何度も何度も繰り返さなければ理解しようがないのではないでしょうか。
数学は周回ゲー
周回ゲー(周回プレイ)という言葉があります。同じゲームや同じステージを何回も繰り返し遊ぶうちに、ゲーム内での資産やプレイヤーとしての経験値が蓄積して、だんだんと効率的に周回できるようになっていく。
数学はまさに周回ゲーです。初見プレイでは非常に難しく理解できない部分が多いが、何度か周回するうちに見覚えのある話が増えていき、身につけられた部分が少しずつ増えていきます。
死に覚えゲーと言っても良いでしょう。最初は理不尽に見える仕掛けも、パターンを理解すればあっさり解けるようになってしまったします。「全然わからない」状態がクリアできた瞬間は、学んでいてとても気持ちがいいです。
ツイッターで、数学書に関するジョークのツイートを見かけました。数学の英語の専門書と言えば、この黄色い本、シュプリンガー(出版社)は有名です。
Basically every math textbook pic.twitter.com/3tXCphcz0G
— Davide Castelvecchi (@dcastelvecchi) May 18, 2022
Introduction to That Thing
But only for people who already know it
あれこれ入門
ただし、それを既に知っている人向け
大学数学で「~~入門」というタイトルの本を真面目に読んだことがある人は、この文句に共感しやすいのではないでしょうか。
僕は学部生時代に次の本を読みましたが、確かに初学者向けではない、「既に知っている人」向けの本だなと思います。
東京大学出版会 (1966-03-31T00:00:01Z)
¥635 (中古品)
東京大学出版会 (2019-03-08T00:00:00.000Z)
¥2,750
参考:大学数学の教科書(数学書)が難しいのはなぜ? 読み方を考える
しかし、誰だって最初は知らない人であって、繰り返し本を読むうちにだんだんと「既に知っている人」になっていくわけです。最初から既習者ではありえず、その過程こそが数学の学習と言えます。
僕はこれらの本を読むために、他のよりやさしい線形代数や微積分の本を何冊か読みました。違う観点から書かれた本を何冊も読んで周回することで、だんだんと「既に知っている人」になっていったのです。
線形代数や微積分に限らず、数学のより専門的な分野を新たに学ぶときも、僕はこの学習の仕方をしています。1回きりの学習、1冊だけの本ではとても理解しきれないのが普通です。ほんの1ページ、1部分でもわかる部分を自分のものにし、少しずつわかる範囲を増やしていくことで、自分の中に理論を作り上げていきます。
この例は大学数学ですが、中学や高校の数学を学ぶときも同じ考え方で身につけてきました。
数学IIICの内容を1周終わらせたのは、高校2年の終わり頃です(学校のカリキュラム的には、高3の夏でした)。その後受験勉強を通して、苦手な内容を復習していくことで、少しずつできる内容を増やしていました。
中高一貫の進学校では、中学段階で高校の数学を学んだり、高校1年のうちに高校の数学の内容を一周終わらせていたりします。余った時間で何回か復習することで、身につけられる内容が増えるわけです。
逆に言えば、ほぼ一周しかできなければ、頭の良い人ですら身につけるのは難しいでしょう。何周もしていない段階で数学が身についていないからといって、「自分には数学の才能がない」なんて思わないでください。当たり前のことなのです。
1回で完璧に身につけるなんて、無理なんです。まずはそこを認めましょう。できなくても当然です。「数学は基礎だから、できなければならない」という思い込みも捨てましょう。完璧主義的に学ぶ必要も別にないのです。
数学に限らず、自分の興味のあることを学び進めましょう。そこでどうしても数学が必要になったら、そのときに復習すれば、自然と中学や高校の数学を周回することになります。僕も大学数学を学ぶ中で、何回も中学や高校の数学を学び直すことになりました。数学を駆使するのに、最初から得意である必要はないのです。
わかっていないことに気づいたら、どれだけ前の内容だろうが遡って足元を固めていきましょう。それが結果的に、数学を学ぶ最短の道になります。
効率やコスパを目的としすぎない
学ぶのが苦手なのだろうなという人の特徴に、「学びに効率性ばかり求める」ことがあります。曰く、「三角関数なんて社会に出ても何の役にも立たない」「数学のコスパの良い勉強法が知りたい」、と。
「学ぼうとしている数学が何の役に立つのか」「必要になる数学だけを効率よく学べないか」という疑問そのものは良いです。自分なりの疑問を持ちながら勉強をするのは、非常に良い姿勢だと思います。
しかし、数学のような基礎学問を学ぶときは、「すぐに役に立つ」を求めて焦りすぎると(いわゆる選択と集中)、結果として「全部役に立たない」という結論に陥りやすいです。
数学、基礎学問、理論、科学は、日常生活や社会に応用されるまでに、多くのステップと時間がかかります。

「数学は物理の役に立つ。物理は工学の役に立つ。工学は社会の役に立つ」といったロジックを理解するには、数学、物理、工学を幅広く教養として学ぶ必要があります。「役に立つ」と感覚的に思える全体像が見えるには、深い理解と広い実践が必要なのです。
これは非常に難しいことです。中学高校での数学の教科書は、応用の話が少なく、数学の話に閉じているように見えます。これはあまり良いことだとは僕は思っておらず、「多くの人が数学を学ぶことに意味がある」と感じてほしいとは思っています。しかし、そのためには広い範囲のことを学ばなければならず、結果的に難しくならざるをえません。
まず数学の内容にフォーカスして学ぶことは、数学という分野内での理解度を高めます。ひとつ確かな土台を築くことができれば、そこに物理や工学など他の土台を組み合わせることができます。しかし土台が確かでないのにあれもこれもと手を出すと、どれも中途半端で「口だけ」で実践できないようになってしまうでしょう。
一般に、必要なことだけ学ぶよりも、人に教えるために学ぶことのほうが深く広い学びが求められます。例えば小学校の算数をきちんと教えるために、中学高校大学の数学を、知れば知るほど、「これは何々に使うんだよ」と教えられる幅が広がるでしょう。
「この数学は~~に役立つ」と教えられるようになるのは、非常に難しいことです。学び始めの人は、なおさらその問題を解決するのは難しいでしょう。何しろ全体像を知らないのですから。
だから最初は、地図(ロードマップ)を自分なりに作り上げることを意識し、そこから「役に立つ」をすぐに取り出そうとしないことです。「数学はすぐに役に立たない」と言っているわけではありません。
学ぶことはある種の投資で、大きなリターンを得るには、最初に思考と時間をつぎ込んでおく必要があります。よほどの天才でない限り、最初から大きな利益が出るものではないので、小さくても確実に積み立てていく感覚を楽しみましょう。何周もした経験は自分の中に残っていくので、やがて勉強したことの恩恵がいかに大きいか気づく瞬間が訪れるでしょう。
以上、数学で学ぶことや覚えることが多すぎることへの対処法として、時間をかけて周回するのが結果として最短になることを紹介してきました。
頭を使って考えるスキルは、数学をするにしても何をするにしても必要です。確かに学ぶ内容は多いかもしれませんが、焦らずに自分のペースで積み重ねていけば、結果的に短い期間で多くの問題を数学的に解けるようになるでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
東京大学出版会 (1966-03-31T00:00:01Z)
¥635 (中古品)
東京大学出版会 (2019-03-08T00:00:00.000Z)
¥2,750
参考:大学数学の教科書(数学書)が難しいのはなぜ? 読み方を考える
森北出版 (2022-03-08T00:00:01Z)
¥1,980
こちらもおすすめ
多すぎる数学の宿題に意味はない? わかるコツは「やらされない」こと
大学数学の教科書(数学書)が難しいのはなぜ? 読み方を考える