どうも、木村(@kimu3_slime)です。
今回は、交流回路で電流電圧の位相がずれる理由について、微分による説明をします。
交流電源を持つ回路を考えましょう。コイルやコンデンサーを含むと、そこでは電流と電圧の位相のずれが生じます。

画像引用:実戦物理重要問題集 物理基礎・物理
90°(\(\frac{\pi}{2}\))だけ位相がずれるのはなぜでしょうか。これを説明していきます。
コイルの場合
まず、交流とは電圧が正負に周期的に変化するものです。電源の電圧を、\(E = V_0 \sin \omega t\)としましょう。
インダクタンス\(L\)のコイルと交流電源のみの回路を考えましょう。コイルによる電圧は、\(E_L = L\frac{dI}{dt}\)です。
したがって、キルヒホッフの第2法則(電圧保存)から、
\[E_L =E\]
\[L\frac{dI}{dt} = V_0 \sin \omega t\]
です。これを満たす電流\(I(t)\)を求めると、微分してサインになるので、
\[ I(t) = – \frac{V_0}{\omega L} \cos \omega t\]
となりました。
電圧\(E = V_0 \sin \omega t\)と位相を比較しましょう。\(\sin \omega t = \cos (\omega t – \frac{\pi}{2})\)なので、電圧が電流よりも\(\frac{\pi}{2}\)の位相だけ先に進んでいることがわかりました。
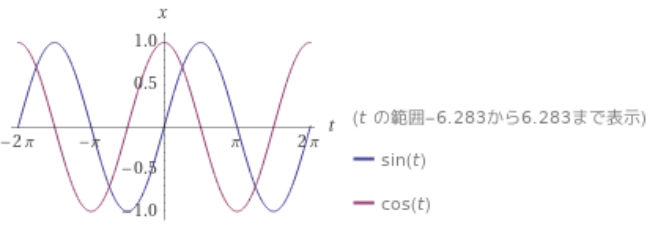
画像引用:WolframAlpha
コンデンサーの場合
電気容量\(C\)のコンデンサーを持つ交流回路について、同様に考えていきましょう。
コンデンサーの電圧は、\(E_C =\frac{1}{C}Q\)です。
したがって、キルヒホッフの第2法則から、
\[E_C =E\]
\[\frac{1}{C}Q = V_0 \sin \omega t\]
です。ここで、電気量の時間変化率が電流 \( \frac{dQ}{dt}=I \)なので、両辺を微分すると
\[ \frac{1}{C} I(t) = \omega V_0 \cos \omega t\]
\[I(t) = \omega C V_0 \cos \omega t\]
となります。
電流の位相\(\cos \omega t\)を基準にすると、電圧の位相\(\sin \omega t\)は、\(\sin \omega t = \cos (\omega t -\frac{\pi}{2})\)なので、電流が電圧よりも\(\frac{\pi}{2}\)だけ進んでいることがわかりました。

画像引用:WolframAlpha
まとめ
まとめると、ずれが生じるポイントは、コンデンサーとコイルの電圧の定義において、微分が含まれることによるものでした。
コンデンサーでは、\(E_L = L\frac{dI}{dt}\)となり、電流の変化率が電圧に影響します。三角関数が変化率最大となるのは、\(\sin x\)の\(x=0\)のところなので、電圧のほうが先に変化していることがわかりますね。
コイルでは、\(I =\frac{dQ}{dt} = C \frac{dE}{dt}\)となり、電圧の変化率が電流に影響します。さきほどのケースの入れ替わりで、電流のほうが先に変化していますね。
逆に見れば、電圧電流の\(\frac{\pi}{2}\)が位相差が実験的得られたとして、それを理論的に表現するために、微分や三角関数が利用できるとも言えるでしょう。
以上、交流回路で電流電圧の位相がずれる理由について、微分による説明をしてきました。
コンデンサーは電圧の変化を妨げる、コイルは電流の変化を妨げると言っても良いですが、それを数式で理解するために、今回の話が役に立てば嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
数研出版 (2021-11-06T00:00:01Z)
¥1,990 (コレクター商品)