球の体積、三平方の定理の応用：金属結晶の充填率の求め方

どうも、木村（@kimu3_slime）です。

小学校や中学校の算数数学では、球の体積の求め方や、三平方の定理を学びます。これらは幾何学の問題以外に、何に使うのでしょうか。

今回は、球の体積計算、三平方の定理の応用として、金属結晶の充填率の求め方を紹介します。

金属結晶の充填率の求め方

金属は、ごく小さなスケールでは、結晶として規則正しく粒子が並んでいることが知られています（金属結晶）。

粒子の三次元的な並び方を表したものは、結晶格子と呼ばれています。

今回は、次のような結晶格子、面心立方格子（face-centered cubic）を考えましょう。

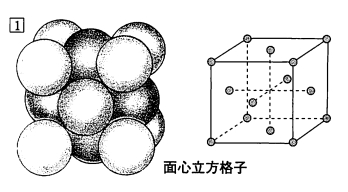
画像引用：化学の新研究

結晶格子の一部分、繰り返すパターンの最小単位を取り出したものは単位格子と呼ばれています。

面心立方格子は、立方体の形をした格子で、その角と面の中心に原子があるのでそう呼ばれているわけです。アルミニウム、銅、銀などが面心立方格子の例です。

面心立方格子の単位格子において、立方体の体積に対する原子の体積の占める割合、充填率を求めてみましょう。

原子は完全な球と仮定し、その半径を\(r\)とします。単位格子の一辺の長さ、格子定数を\(a\)とします。

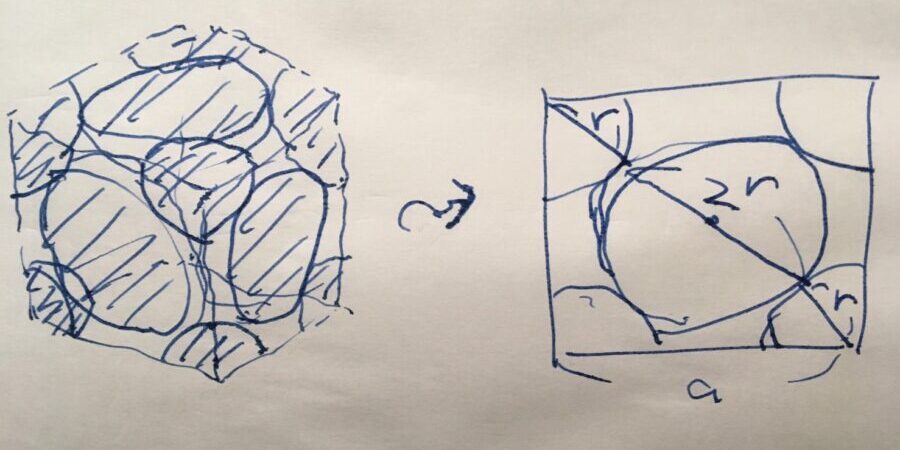
立方体の体積は、\(a^3\)です。

原子の占める体積は、半分の球が6個、1/8の球が8個あります。ひとつの球の体積は、\(\frac{4}{3}\pi r^3\)です。したがって、合計の体積は\(\frac{4}{3}\pi r^3 (\frac{1}{2}\times 6 +\frac{1}{8}\times 8)=\frac{16}{3} \pi r^3\)となります。

これらの比を計算するには、\(a,r\)の関係がわかると良いです。そこで上に書いた図を見ましょう。原子の中心は面の中心にあり、したがって面の対角線上で接する作りになっています。対角線の長さは、半径の合計で、\(r+2r+r=4r\)です。よって、三平方の定理（ピタゴラスの定理）から、

\[a^2 +a^2 = (4r)^2\]

\[a= 2\sqrt{2} r\]

となります。\(a,r>0\)であることに注意。

よって、充填率は

\[\begin{aligned} 充填率 &= \frac{原子の占める体積}{単位格子の体積} \\&=\frac{\frac{16}{3}\pi r^3}{a^3}\\ &=\frac{\frac{16}{3}\pi r^3}{16\sqrt{2} r^3}\\&= \frac{\sqrt{2}}{6}\pi \\&\approx 74 \% \end{aligned}\]

と求めることができました。

これは格子定数\(a\)、原子半径\(r\)によらない値です。面心立方格子ならば、常に充填率が約74%になることがわかりますね。

以上、球の体積計算、三平方の定理の応用として、金属結晶の充填率の求め方を紹介してきました。

充填率や密度、重さの計算は、幾何学の良い応用問題になります。球の面積や三平方の定理の応用として、金属の結晶の話は面白いと思います。

木村すらいむ（@kimu3_slime）でした。ではでは。