どうも、木村(@kimu3_slime)です。
高校までの化学で数学を使う印象はあまりないかもしれませんが、大学の化学では欠かせないものとなります。
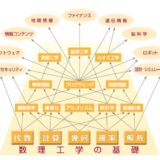
今回は、大学で化学を学ぶために学ぶために必要な大学数学の一覧を紹介します。
東京大学理学部化学科のカリキュラムと山本雅博「物理化学で使う数学はこれで充分」を参考に書いています。僕の大学時代の専門は数学であり、化学に関しては専門でないことをご了承ください。
化学と数学の関係
高校化学と大学の化学の違いとしては、まず物理の考え方を積極的に利用することにあるでしょう。特に、熱力学と量子力学という分野が、化学が扱う大きさ・スケールにおいて重要です。
化学物質は実に多様なものですが、分野としてはおおざっぱに、無機化学、有機化学、高分子化学に分かれます。それらに共通するのが、化学物質がどんな状態にあるかを測定・分析する理論、分析化学です。
その分析には、そもそも化学物質がどんな物理法則に従っているのか、化学反応では何が起こっているかを知る必要があります。そこで扱われるのが、化学熱力学や量子化学といった物理化学です。
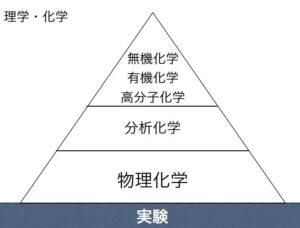
参考:山本雅博「物理化学で使う数学はこれで充分」
大学の数学は、化学の基礎、特に物理化学や分析化学の理解に必要になってくるでしょう。
教養数学
教養数学は、大学1年で教養として学ぶことが多い数学科目です。
微分積分学
例えばメタンガスを酸素と結びつける(燃やす)と、熱が発生し、二酸化炭素と水に変わっていきます。化学反応では、前後で状態が変化します。
このような変化を扱うのが、微分と積分の理論です。特に熱力学では、温度や圧力など複数の変数を考え、偏微分・全微分を利用することになるでしょう。シュレーディンガー方程式はある種の微分方程式であり、その理解にも微分積分は欠かせません。
線形代数学
高校物理ではニュートンの運動方程式や力学を学びましたが、原子や電子レベルのミクロな世界では、シュレーディンガー方程式や量子力学が重要な法則となってきます。電子軌道やスピン、化学結合について知るためには、量子力学が欠かせません。熱力学がマクロ化学なら、量子力学がミクロ化学でしょう。
その量子力学を理解するための数学的基礎のひとつが、線形代数学です。シュレーディンガー方程式を解くのは、一般には難しいのですが、そこで単純化、線形的に近似します。
そこで現れるのは行列の固有値・固有ベクトル(固有ベクトル)といった考え方になります。線形代数の最初では、数ベクトル空間を扱うと思いますが、その考え方が量子力学で扱うような固有関数の理解の基礎となるでしょう。
線形代数とセットで、量子力学の理解に欠かせない複素数の扱いもセットで学ぶことになるでしょう。
統計学
化学において、実験とその計画はとても重要です。僕の化学系の友人は、多くの時間を科学実験に費やしていた印象があります。
実験に誤差はつきものですが、その誤差を適切に扱うためには、統計学の知識が必要となるでしょう。それは分析化学につながってきます。
統計学は、例えば気体を原子の集合体として見たとき、その全体の挙動を統計的に捉える分野、統計熱力学の理解にもつながってくるでしょう。
専門数学
微分方程式
化学反応がどのくらいのスピードで進むか、どんな関数で表されるかといった問題は、反応速度論と呼ばれる分野で扱われます。その問題は数学的には微分方程式で表されるので、その解き方を学びましょう。
微分方程式は常微分方程式と偏微分方程式に分けられますが、量子力学におけるシュレーディンガー方程式、電磁気学におけるマクスウェルの方程式は後者です。
化学における微分方程式の問題は、結局は常微分方程式か線形代数、コンピュータによる解法に帰着されることが多いかもしれません。が、その基礎として偏微分方程式を知っておくと理解が深まるでしょう。
発展的な話題ですが、BZ反応と呼ばれる周期的な化学反応は面白いです。ぜひ見てみてください。
これは数学的には、反応拡散方程式と呼ばれる偏微分方程式によってモデル化されます。
参考:生き物の模様は数式で決まる? チューリング・パターンとは、花粉の広がりを数式で予測する、拡散方程式とは
群論、抽象代数学
分子や結晶は、その種類に応じて何らかの規則性や対称性を持っています。そうした対称性を数学的に表すと、群(ぐん)と呼ばれるものの集まりになります。
例えば、アンモニア\(\mathrm{NH_3}\)は3回の平面回転\(C_3\)で、回転軸を通る面に関して鏡映対称(垂直)なので、\(C_{3v}\)という記号で表されます。
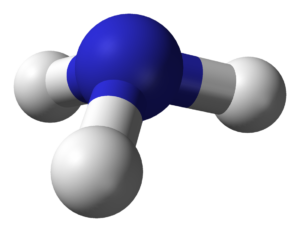
画像引用:Ammonia-3D-balls-A.png, – Wikipedia
化学における群論は、点群・結晶群と呼ばれ、シェーンフリース記号(Schönflies notation)やヘルマン・モーガン記号(Hermann–Mauguin notation)といった群を表す記号が使われています。
参考:図形の対称性を記述する二面体群、多面体群、点群・結晶群について解説
以上、化学を学ぶために必要な大学数学を紹介してきました。
せっかく大学で基礎から化学を学ぶからには、物理や数学といった基礎も合わせて学ぶと、より化学そのものの理解が深まるのではないでしょうか。
木村すらいむ(@kimu3_slime)でした。ではでは。
裳華房 (2019-11-15T00:00:00.000Z)
¥3,135
Donald A. McQuarrie(著), 藤森 裕基(翻訳), 松澤 秀則(翻訳), 筑紫 格(翻訳)
丸善出版 (2014-03-21T00:00:01Z)
¥4,180
こちらもおすすめ
図形の対称性を記述する二面体群、多面体群、点群・結晶群について解説