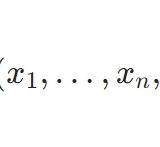区間推定、信頼区間とは：分散既知の正規分布における平均の推定を例に

どうも、木村（@kimu3_slime）です。

今回は、区間推定、信頼区間とは何か、分散既知の正規分布における平均の推定を例に紹介します。

区間推定とは
信頼区間とは
分散既知の正規分布における平均の推定
こちらもおすすめ

区間推定とは

区間推定（interval inference）は、統計モデルのパラメータを推測する統計的推測の一種です。

点推定ではパラメータを$\hat{\mu} = 46$のようにピンポイントで推定しますが、区間推定では$41 < \mu < 52$のようにある区間内にある確率が高いと推定します。その推定に使う区間は、信頼区間と呼ばれます。

信頼区間とは

信頼区間の考え方を、より明確にしましょう。パラメータ$\theta$をもつある母集団分布があり、そこから$n$個のランダムなサンプルが得られたとします。

そのサンプルから何かしらの計算をして、パラメータは「$49 < \theta < 51$という範囲に必ず含まれる」と言うことができるでしょうか？　ありえませんね。サンプルにはランダム性があるので、推測した区間がたまたまズレていたという可能性がありえます。

しかし、次のようなことなら確実に言えそうです。「サンプルからある手順で区間を求める操作を何度も繰り返せば、パラメータがその区間の範囲に95%の確率で含まれる」。個別には外れる可能性はありますが、その可能性は小さく、高確率でパラメータが含まれる範囲を推測できています。

確率$\gamma$で$\theta$が$\theta_1 < \theta < \theta_2$に含まれることを、$\mathrm{CI}_{\gamma} (\theta_1 < \theta < \theta_2)$と書き、それを$\theta$の$100 \gamma$%信頼区間（CI; confidence interval）と呼びます。単に開区間$(\theta_1, \theta_2)$が信頼区間であるとも呼ばれます。

$\gamma$は信頼水準（confidence level）と呼ばれるものです。$\gamma= 0.95,0.99$が選ばれることは多く、それぞれ95%信頼区間、99%信頼区間と呼ばれます。

信頼区間の端点を信頼限界（confidence limit）と呼びます。$\theta_1$が下側信頼限界（LCL; lower confidence limit）、$\theta_2$が上側信頼限界（UCL; upper conficence limit）です。

信頼区間の定義を確率の言葉を使って言い表せば、次のようになります。$P$を母集団分布の確率測度として、$X_1,\dots,X_n$をその分布に従う独立な確率変数族とします。$\theta_1,\theta_2$を$X_1,\dots,X_n$により決まる統計量としましょう。

信頼区間が$\mathrm{CI}_{\gamma} (\theta_1 < \theta < \theta_2)$であるとは、すべての$\theta$に対し、

\[P(\theta_1 < \theta < \theta_2)= \gamma\]

が成り立つことです。

分散既知の正規分布における平均の推定

信頼区間とはどのようなものなのか、より具体的に見ていきましょう。

簡単な例として、母集団分布は正規分布であり、その分散$\sigma^2$が既知であるケースについて考えます。このとき、母集団分布の平均$\mu$（未知とする）を区間推定してみましょう。

分散を知っているという仮定は強力で非現実的かもしれませんが、まずは簡単なケースで考え方を理解していきましょう。

一般的な性質として、標本誤差$Z_n =\frac{M_n -\mu }{\frac{\sigma}{\sqrt{n}} }$は標準正規分布に従うことが知られています（近似でなく従うのは、母集団分として正規分布を考えていることによる）。したがって、$c>0$として

\[P(-c < Z < c )= \Phi(c)-\Phi(-c)\]

が成り立ちます。これを利用して、信頼区間を求めてみましょう。

まず左辺に注目して、$\mu$に関する区間として書き換えます。

$-c<Z<c$は、$-c \frac{\sigma}{\sqrt{n}}<M_n-\mu < c \frac{\sigma}{\sqrt{n}}$と同値です。これを整理すれば、$ M_n – c\frac{\sigma}{\sqrt{n}}< \mu < M_n + c\frac{\sigma}{\sqrt{n}}$となりました。

$\Phi(c)-\Phi(-c) = \gamma$を満たす$c$を求めれば、

\[P(M_n – c\frac{\sigma}{\sqrt{n}} <\mu < M_n + c\frac{\sigma}{\sqrt{n}})= \gamma\]

なので、$\mathrm{CI}_{\gamma}( M_n – c\frac{\sigma}{\sqrt{n}} <\mu < M_n + c\frac{\sigma}{\sqrt{n}})$と信頼区間が求められます。

$\Phi(c)-\Phi(-c) = \gamma$を満たす$c$の近似値は、よく用いる$\gamma$については知られています。

$\gamma$	$0.90$	$0.95$	$0.99$	$0.999$
$c$	$1.645$	$1.960$	$2.576$	$3.291$

コンピュータ（Julia）を使えば、指定された$\gamma$に対し、次のようにして$c$を求めることができます。

using Distributions
Γ = [0.9,0.95,0.99,0.999]
for γ in Γ
println(quantile(Normal(0,1), (γ+1)/2))
end

using Distributions

Γ = [0.9,0.95,0.99,0.999]

for γ in Γ

println(quantile(Normal(0,1), (γ+1)/2))

end

1.6448536269514717
1.9599639845400576
2.5758293035489053
3.290526731491931

1.6448536269514717

1.9599639845400576

2.5758293035489053

3.290526731491931

「quantile(Normal(0,1), w)」が標準正規分布の累積分布関数$\Phi(z)$の逆関数$\Phi^{-1}(w)$です。$\Phi(c)-\Phi(-c) = 2\Phi(c)-1$なので、$2\Phi(c)-1 =\gamma$より$c= \Phi^{-1}(\frac{\gamma+1}{2})$となっています。

参考：対称な確率密度関数を持つ累積分布関数の計算

より具体的に、95%信頼区間を求めてみます。

分散は$\sigma^2 =100$で、20個のサンプル$x_1,\dots,x_{20}$を取ったとしましょう。

using Distributions,Random
d1 = Normal(50,10)

Random.seed!(2022)
x = rand(d1,20)

using Distributions,Random

d1 = Normal(50,10)

Random.seed!(2022)

x = rand(d1,20)

20-element Vector{Float64}:
 50.6912301164913
 38.84399961848597
 42.84480604223728
 60.9769650429804
 54.978651946367876
 33.951339022096505
 40.96806064167559
 32.42960541746047
 49.11909337153176
 48.368593011534614
 45.130463442688736
 66.0313475290611
 69.28907743700123
 39.33330176391247
 42.431065464081925
 54.22677747724986
 33.47032914639008
 54.43764421449241
 43.595211148546284
 25.114095856632616

20-element Vector{Float64}:

50.6912301164913

38.84399961848597

42.84480604223728

60.9769650429804

54.978651946367876

33.951339022096505

40.96806064167559

32.42960541746047

49.11909337153176

48.368593011534614

45.130463442688736

66.0313475290611

69.28907743700123

39.33330176391247

42.431065464081925

54.22677747724986

33.47032914639008

54.43764421449241

43.595211148546284

25.114095856632616

95%信頼区間を考えているので、$\gamma= 0.95$で、$c \approx 1.960$です。母集団の標準偏差は、$\sigma =10$となっています。サンプル平均は$M_{20} \approx 46.3$です。

信頼区間$\mathrm{CI}_{\gamma}( M_n – c\frac{\sigma}{\sqrt{n}} <\mu < M_n + c\frac{\sigma}{\sqrt{n}})$を計算すると、

n = length(x)
σ = 10
γ = 0.95
c = quantile(Normal(0,1), (γ+1)/2)
LCL = mean(x)-c*σ/sqrt(n)
UCL = mean(x)+c*σ/sqrt(n)
println("($LCL, $UCL)")

n = length(x)

σ = 10

γ = 0.95

c = quantile(Normal(0,1), (γ+1)/2)

LCL = mean(x)-c*σ/sqrt(n)

UCL = mean(x)+c*σ/sqrt(n)

println("($LCL, $UCL)")

(41.928970182663, 50.69419558842883)

1	(41.928970182663, 50.69419558842883)

と95%信頼区間を求めることができました。このケースでは、母集団の平均$\mu =50$が区間内に入っていますね。

「20個サンプルを取り出して信頼区間を計算する」試行を、20回繰り返してみます。

k = 20
μ = 50
σ = 10
γ = 0.95
c = quantile(Normal(0,1), (γ+1)/2)
in_interval = 0
for i in 1:k
    x = rand(d1,20)
    n = length(x)
    LCL = mean(x)-c*σ/sqrt(n)
    UCL = mean(x)+c*σ/sqrt(n)
    println("($LCL, $UCL)")
    if LCL < μ < UCL
        in_interval +=1
    else    
    end
end
println(in_interval/k)

k = 20

μ = 50

σ = 10

γ = 0.95

c = quantile(Normal(0,1), (γ+1)/2)

in_interval = 0

for i in 1:k

x = rand(d1,20)

n = length(x)

LCL = mean(x)-c*σ/sqrt(n)

UCL = mean(x)+c*σ/sqrt(n)

println("($LCL, $UCL)")

if LCL < μ < UCL

in_interval +=1

else

end

println(in_interval/k)

(47.19238949336922, 55.95761489913505)
(45.92246060406128, 54.68768600982711)
(46.30697763211043, 55.072203037876264)
(45.374685735504514, 54.139911141270346)
(46.61174264274234, 55.376968048508175)
(44.18399577753221, 52.94922118329804)
(43.555051773549806, 52.32027717931564)
(44.34360269209448, 53.10882809786031)
(49.80914273447218, 58.574368140238015)
(49.6718904630829, 58.437115868848736)
(44.21597945544641, 52.98120486121224)
(43.91550969307136, 52.68073509883719)
(43.52139605039384, 52.28662145615967)
(44.08964331266732, 52.85486871843315)
(47.89027052959545, 56.65549593536128)
(47.573601743088005, 56.33882714885384)
(42.06499561354677, 50.8302210193126)
(43.169193971345955, 51.93441937711179)
(40.855680391401876, 49.62090579716771)
(45.95504294081468, 54.72026834658051)
0.95

(47.19238949336922, 55.95761489913505)

(45.92246060406128, 54.68768600982711)

(46.30697763211043, 55.072203037876264)

(45.374685735504514, 54.139911141270346)

(46.61174264274234, 55.376968048508175)

(44.18399577753221, 52.94922118329804)

(43.555051773549806, 52.32027717931564)

(44.34360269209448, 53.10882809786031)

(49.80914273447218, 58.574368140238015)

(49.6718904630829, 58.437115868848736)

(44.21597945544641, 52.98120486121224)

(43.91550969307136, 52.68073509883719)

(43.52139605039384, 52.28662145615967)

(44.08964331266732, 52.85486871843315)

(47.89027052959545, 56.65549593536128)

(47.573601743088005, 56.33882714885384)

(42.06499561354677, 50.8302210193126)

(43.169193971345955, 51.93441937711179)

(40.855680391401876, 49.62090579716771)

(45.95504294081468, 54.72026834658051)

0.95

19回が区間内に$\mu=50$が含まれていて、1回（(40.855680391401876, 49.62090579716771)）だけ含まれていません。ほとんどのケースで、信頼区間内に真のパラメータの値があります。

相対頻度（経験確率）は、$\frac{19}{20}=0.95$になっています。この頻度はぴったりになるとは限りませんが、試行を増やせばその値に近づいていきます。例えばk=10000を試すと、0.95012となりました。これが信頼区間の意味です。

信頼水準と信頼区間の幅（大きさ）は、トレードオフの関係にあります。つまり、信頼水準を厳しくする（正しい確率の高い区間推定にする）と、信頼区間の幅は広がります。

信頼区間の幅は、上側信頼限界から下側信頼限界を引いて

\[ \begin{aligned} &\quad (M_n + c\frac{\sigma}{\sqrt{n}})- (M_n – c\frac{\sigma}{\sqrt{n}})\\&= 2c\frac{\sigma}{\sqrt{n}}\end{aligned}\]

です。

極端な話、$\gamma \to 1$とすれば、$c \to \infty$となり、信頼区間は実数全体となります。「平均は100％の確率でいずれかの実数を取る」は正しいですが、無意味な推測です。

20個の同じサンプルについて、信頼水準を変えて、信頼区間とその幅を計算してみましょう。

σ = 10
n = length(x)
Γ = [0.9,0.95,0.99,0.999]
for γ in Γ
    c = quantile(Normal(0,1), (γ+1)/2)
    LCL = mean(x)-c*σ/sqrt(n)
    UCL = mean(x)+c*σ/sqrt(n)
    println("($LCL, $UCL)")
    println(UCL-LCL)
end

σ = 10

n = length(x)

Γ = [0.9,0.95,0.99,0.999]

for γ in Γ

c = quantile(Normal(0,1), (γ+1)/2)

LCL = mean(x)-c*σ/sqrt(n)

UCL = mean(x)+c*σ/sqrt(n)

println("($LCL, $UCL)")

println(UCL-LCL)

end

(45.91886022453523, 53.274869270336374)
7.3560090458011445
(45.214252044552886, 53.97947745031872)
8.765225405765833
(43.83713532626451, 55.356594168607096)
11.519458842342587
(42.23902329403965, 56.95470620083196)
14.71568290679231