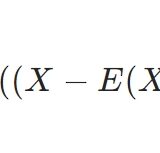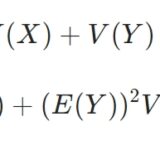確率変数の相関係数が-1以上1以下であることの証明

どうも、木村（@kimu3_slime）です。

今回は、確率変数の相関係数が-1以上1以下であることの証明を紹介します。

\[-1\leq \mathrm{Cor}(X,Y) \leq 1\]

期待値の積による内積
コーシー・シュワルツの不等式の適用
こちらもおすすめ

期待値の積による内積

相関係数が内積の定義を満たすことを示せれば、コーシー・シュワルツの不等式から結論が導けます。

そのために、期待値の積\(\langle X, Y\rangle := E(XY)\)が内積の定義を満たすことをまず示しましょう。

内積を考えるには、舞台となる線形空間が必要です。

確率変数\(X\)とは、（可測な）実数値関数\(X:\Omega \to \mathbb{R}\)でした。その集合上に和とスカラー倍

\[(X+Y)(\omega) = X(\omega)+Y (\omega)\]

\[(cX) (\omega) = cX(\omega)\]

を定めることで、線形空間（関数空間）が定まります。

特に今回は共分散を考えたいので、\(X^2 \)の期待値（原点まわりの2次のモーメント）が有限である部分空間を考えましょう。

\[\|X\|_2 := \sqrt{E(X^2)}\]

と置き、

\[ V = \{f :\Omega \to \mathbb{R} \mid \|X\|_2 <\infty\}\]

とすると、\(V\)は\(\|\cdot\|_2\)をノルムとする線形空間になります。

（ほぼ\(L^2 (\Omega)\)が線形空間となる理由と同じです。）

\(V\)において、\(\langle X, Y\rangle := E(XY)\)が内積の定義

任意の\(X,Y, Z\in V\)、\(\lambda \in \mathbb{R}\)に対し、
(1) 対称性：\(\langle X,Y\rangle =\langle X,Y\rangle\)
(2) （二重）線形性：\(\langle \lambda X+Z,Y\rangle = \lambda \langle X,Y\rangle +\langle Z,Y\rangle\)
(3) 正定値性：\(\langle X,X\rangle \geq 0\)。\(a\neq 0\)ならば\(\langle X,X\rangle > 0\)。

を満たすことを確かめましょう。

実数の積は可換なので、\(XY = YX\)が成り立ちます。したがって、\(E(XY)=E(YX)\)なので、対称性を満たします。

期待値は加法性と定数倍の性質（線形性）を持ちます。したがって、

\[\begin{aligned} &\langle \lambda X+Z,Y\rangle \\&= E((\lambda X+Z) Y ) \\&= \lambda E(XY)+ E(ZY) \\&= \lambda \langle X,Y\rangle +\langle Z,Y\rangle \end{aligned}\]

が成り立ちます。

\(\langle X,X\rangle = \| X\| _2\)なので、ノルムの正定値性から内積の正定値性が導かれます。

よって、\(\langle X, Y\rangle := E(XY)\)が内積の定義を満たすことが示せました。