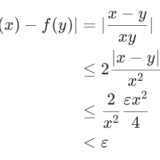どうも、木村(@kimu3_slime)です。
今回は、写像・関数の像の定義、例と求め方(一点集合、区間)を紹介します。
逆像の定義
\(X,Y\)を集合とし、写像(関数)\(f:X \to Y\)について考えます。
\(A \subset X\)とし、部分集合\(A\)の\(f\)による像(image, range)は、
\[f(A):= \{y \in Y \mid y=f(x) となるx \in Aが存在する\}\]
と定義される\(Y\)の部分集合です。
言い換えれば、\(A\)の要素\(x\)を動かしたときの値\(f(x)\)の集合ですね。像はしばしば、
\[f(A):= \{f(x) \in Y \mid x\in A\}\]
と省略して表記されます。
また、定義域全体の像は
\[\mathrm{Im }(f) := f(X)\]
と表すこともあります。
像の例、求め方、応用
像とは、具体的にはどんなものなのでしょうか。
一点集合の像
簡単なケースとして、実数値関数\(f:\mathbb{R} \to \mathbb{R}\)、\(f(x)= x^2\)の一点集合\(\{2\}\)の像を求めてみましょう。
像の定義をこの場合に当てはめてみると、
\[f(\{2\}):= \{y \in \mathbb{R} \mid y=f(x) となるx \in \{2\}が存在する\}\]
ですが、\(x\in \{2\}\)とは\(x= 2\)ということです。\(f(2) =2^2 =4\)なので、
\[\begin{aligned} f(\{2\})&= \{y \in \mathbb{R} \mid y=f(2) \}\\ &=\{4\}\end{aligned}\]
と求めることができました。
一般化すると、\(a\in \mathbb{R}\)とするとき、一点集合\(\{a\}\)の像は
\[f(\{a\}) = \{f(a)\}\]
となります。つまり、関数の値を要素とする一点集合です。
一点集合の像は、関数の値とほぼ同義であることがわかります。
区間の像
関数の像と値との違いが出てくるのは、一点集合でない部分集合を考えるときです。
\(A= (-1,2)=\{x \in \mathbb{R} \mid -1 <x <2\}\)という開区間の\(f(x)=x^2\)による像を求めてみましょう。
\[f((-1,2))= \{y \in \mathbb{R} \mid y=x^2 となるx \in (-1,2)が存在する\}\]
これはどんな集合でしょうか。図を書いてみると、想像しやすいです。
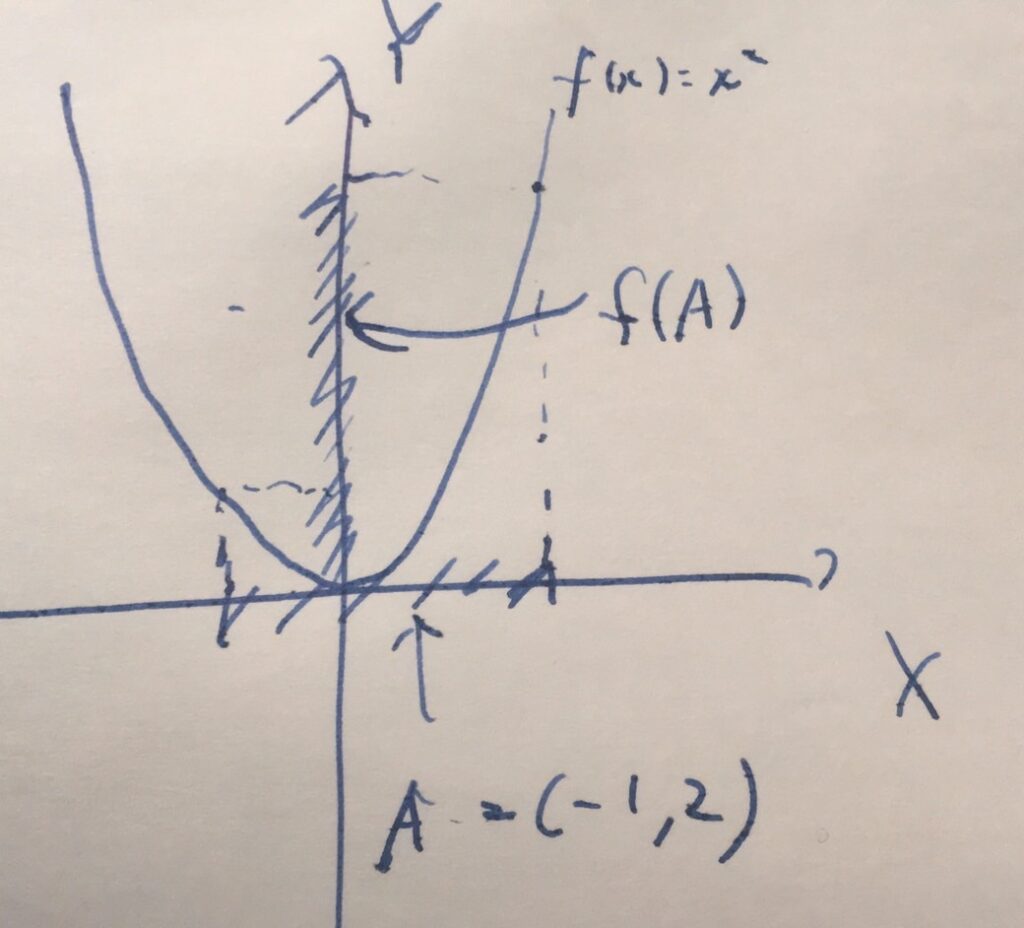
例えば、\(0 \in f((-1,2))\)です。なぜなら、\(0= f(0)\)と表せるからです。また、\(1= f(1)\)となるので、\(1 \in f((-1,2))\)です。
ここから、次のような予想が立てられます。
\[f((-1,2))= [0, 4)\]
これが正しいことを、集合が等しいことの定義にのっとって示しましょう。
\(y \in f((-1,2))\)とすると、\(y=x^2\)となる\(x \in (-1,2)\)が存在します。\(-1 <x <2\)より、\(0\leq x^2 <4\)です(不等式の変形では、単純に各辺を2乗するわけではないことに注意)。したがって、\(y \in [0,4)\)であり、\(f((-1,2))\subset [0, 4)\)です。
逆に、\(y \in [0,4)\)としましょう。\(y \geq 0\)であることに注意して\(x =\sqrt{y}\)と置くと、\(x \in (-1,2)\)であり、\(y= x^2 =f(x)\)が成り立ちます。よって、\(y \in f((-1,2))\)であり、\(f((-1,2))\supset [0, 4)\)です。
以上により、\(f((-1,2))= [0, 4)\)と像が求められました。
関数による定義域の像は、高校数学において、しばしば値域と呼ばれます。値域という言葉は、写像の終域、\(f : X \to Y\)と表すときの\(Y\)としても使われることがあります。これらは別物なので、注意しましょう。
例えば、\(g(x) = \sin x\)による、定義域全体\(\mathbb{R}\)の像を求めてみましょう。グラフを想像すれば、
\[g(\mathbb{R} )= [-1,1]\]
と予想されます。
\(y \in g(\mathbb{R})\)としましょう。\(g(-\frac{\pi}{2}) =-1\)、\(g(-\frac{\pi}{2})= 1\)で、\(-\frac{\pi}{2} < x < \frac{\pi}{2}\)において\(g\)は狭義単調増加なので、\(-1 \leq y = \sin x \leq 1\)です。よって、\(y \in [-1,1]\)。
逆に、\(y \in [-1,1]\)と仮定します。\(g(-\frac{\pi}{2}) =-1< 1=g(-\frac{\pi}{2})\)で、\(-\frac{\pi}{2} \leq x \leq \frac{\pi}{2}\)において\(g\)は連続なので、中間値の定理より\( y= \sin x\)を満たす\(x \in [-\frac{\pi}{2}, \frac{\pi}{2}]\)が存在します。つまり、\(y=\sin x\)を満たす\(x\in \mathbb{R}\)が存在するので、\(y \in g(\mathbb{R} )\)です。
よって、\(g(\mathbb{R} )= [-1,1]\)と示せました。
\(g:\mathbb{R} \to \mathbb{R}\)としても(終域を\(\mathbb{R}\)と考えても)、像(値域)は\(g(\mathbb{R} )= [-1,1]\)です。
最後に、原点での値を指定した逆数関数
\[h(x)= \begin{cases}\frac{1}{x} & (x >0 )\\0 & (x= 0)\end{cases}\]
による閉区間\([0,1]\)の像を求めてみましょう。
グラフを想像してみると、
\[h([0,1])= \{0\} \cup [1, \infty)\]
と予想されます。これが正しいことを証明しましょう。
まず、\(y \in h([0,1])\)と仮定します。像の定義より、\(y= h(x)\)を満たす\(x \in [0,1]\)が存在します。\(x = 0\)のときは\(y=h(0)=0\)なので、\(x \in \{0\}\)です。\( x\neq 0\)のとき、\(x>0\)において\(\frac{1}{x}\)が単調減少であること、\(h(1) =1\)から、\(y=h(x) \geq 1\)、つまり\(y \in [1, \infty)\)となりました。
逆に、\(y \in \{0\} \cup [1, \infty)\)と仮定します。\(y = 0\)のときは、\(h(0)=0 =y\)なので、像の定義から\( y \in h([0,1])\)です。\(y \in [1, \infty)\)のときは、\(y \neq 0\)であることに注意して\(x = \frac{1}{y}\)と置けば、\(y= \frac{1}{x} = h(x)\)です。像の定義から、\(y \in h([0,1])\)です。
よって、\(h([0,1])= \{0\} \cup [1, \infty)\)が示せました。
少し、像を使った発展的な話をしましょう。
\(f\)が連続関数であるとき、連結な集合(つながった集合)の像はまた連結となることが知られています。
\(f(x)= x^2\)による連結な区間\((-1,2)\)の像は、\(f((-1,2))= [0, 4)\)で、確かに連結です。
一方、\(h\)による連結な区間\([0,1]\)の像は、\(h([0,1])= \{0\} \cup [1, \infty)\)と非連結になっています。これは\(h\)が連続でないことを示しています。
また、\(f\)が連続であるとき、コンパクト集合(有界閉集合)の像はまたコンパクトとなることが知られています。
\(f(x)= x^2\)による有界閉集合\([-1,2]\)の像は、\(f([-1,2)])= [0, 4]\)で、確かに有界な閉集合です。
一方、\(h\)による有界閉集合\([0,1]\)の像は、\(h([0,1])= \{0\} \cup [1, \infty)\)と非有界な集合となっています。これもまた、\(h\)が連続でないことを示しています。
以上、写像・関数の像の定義、例と求め方(一点集合、区間)を紹介してきました。
線形代数学では、線形写像(行列)による像を考えます。線形写像による部分空間の像は常に線形空間となり、その次元は線形写像のランクに等しいという一般論があります。
像は数学のあらゆるところで使われる考え方なので、逆像と合わせて具体的に求められるようになると良いでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店 (2018-11-07T00:00:01Z)
¥5,720 (コレクター商品)
こちらもおすすめ
ルートを含む等式の両辺を2乗するときの注意点:逆も成り立つか