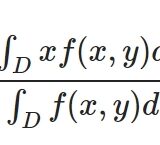どうも、木村(@kimu3_slime)です。
今回は、Julia(SymPy)で偏微分、勾配、発散、回転、合成関数の微分を計算する方法を紹介します。
準備
SymPyを使うので、持っていなければインストールしておきましょう。
1 2 | using Pkg Pkg.add("SymPy") |
準備として、以下のコードを実行しておきます。
1 | using SymPy |
偏微分、勾配
まず、記号として使う変数を用意しておきます。
1 | @vars x y z c t |
\(f_1 (x,y)=x^2+y^2\)のような2変数関数を偏微分してみましょう。
「diff(関数,x)」で\(x\)に関する偏微分、「diff(関数,y)」で\(y\)に関する偏微分です。
1 2 3 | f1 = x^2 + y^2 diff(f1, x) diff(f1, y) |
\[ \begin{aligned}x^{2} + y^{2}\end{aligned} \]
\[ \begin{aligned}2x\end{aligned} \]
\[ \begin{aligned}2y\end{aligned} \]
さらに文字を増やすことで、2階微分や高階の微分を増やせます。
1 2 | diff(f1, x,x) diff(f1, x,y) |
\[ \begin{aligned}2\end{aligned} \]
\[ \begin{aligned}0\end{aligned} \]
同じ変数に関する微分は、「diff(f1, x,2)」といったように表せます。
2変数関数の勾配は
\[ \begin{aligned}\nabla f:=\mathrm{grad} f:=(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y})\end{aligned} \]
と定義されます。これを関数として定義してみましょう。
1 2 3 4 5 | function grad(f) return [diff(f, x),diff(f, y)] end grad(f1) |
\[ \begin{aligned}\left[ \begin{array}{r}2 x\\2 y\end{array} \right]\end{aligned} \]
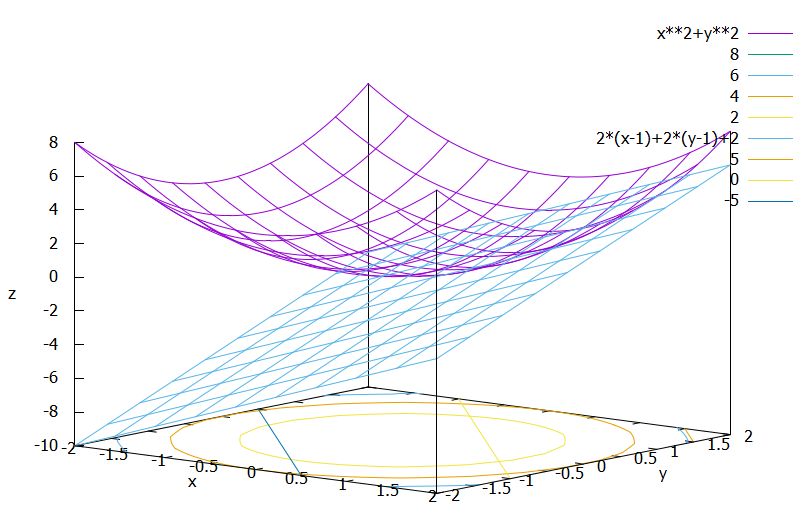
2変数関数\(f\)の点\((a,b)\)における接平面は
\[ \begin{aligned}g(x,y)=f_x(a,b)(x-a)+f_y(a,b)(y-b)+f(a,b)\end{aligned} \]
と表されます。これを計算する関数を作ってみましょう。
関数の特定の値を得る、代入するには、「数式.subs([(x,a),(y,b)])」といったようにします。
1 2 3 4 5 6 7 | function tangent_plane(f,a,b) return (diff(f,x).subs(x,a)*(x-a) + diff(f,y).subs(y,b)*(y-b) +f.subs([(x,a),(y,b)])) end tangent_plane(f1,1,1) |
\[ \begin{aligned}2 x + 2 y – 2\end{aligned} \]
ラプラシアン
\[ \begin{aligned}\Delta u =\frac{\partial^2 u }{\partial x^2}+\frac{\partial^2 u }{\partial y^2}\end{aligned} \]
も同様に定義できますね。
対数ポテンシャル\(\log{\left(\sqrt{x^{2} + y^{2}} \right)}\)のラプラシアンが0である(ラプラス方程式の解である)ことを確かめてみましょう。
1 2 3 4 5 6 7 | function Laplacian(f) return diff(f, x,x)+diff(f, y,y) end f2 = log(sqrt(x^2+y^2)) Laplacian(f2) simplify(Laplacian(f2)) |
\[ \begin{aligned}\log{\left(\sqrt{x^{2} + y^{2}} \right)}\end{aligned} \]
\[ \begin{aligned}\frac{- \frac{2 x^{2}}{x^{2} + y^{2}} + 1}{x^{2} + y^{2}} + \frac{- \frac{2 y^{2}}{x^{2} + y^{2}} + 1}{x^{2} + y^{2}}\end{aligned} \]
\[ \begin{aligned}0\end{aligned} \]
発散、回転
ベクトル値関数(ベクトル場)についても、その値の各成分について同様の偏微分計算ができます。
参考:Julia(SymPy)でベクトルの計算をする方法(内積・ノルム・距離・角度、外積)
1 2 3 | F1 = [y,x] diff(F1[1],x) diff(F1[1],y) |
\[ \begin{aligned}\left[ \begin{array}{r}y\\x\end{array} \right]\end{aligned} \]
\[ \begin{aligned}0\end{aligned} \]
\[ \begin{aligned}1\end{aligned} \]
平面のベクトル場を\(F(x,y)= (F_1(x,y) ,F_2(x,y))\)と表すことにします。その発散
\[ \begin{aligned}\mathrm{div }F:=\frac{\partial F_1}{\partial x}+\frac{\partial F_2}{\partial y}\end{aligned} \]
と回転
\[ \begin{aligned}\mathrm {rot}F =-\frac{\partial F_1}{\partial y}+\frac{\partial F_2}{\partial x}\end{aligned} \]
を計算する関数を作ってみましょう。
1 2 3 4 5 6 7 | function div(F) return diff(F[1],x)+diff(F[2],y) end function rot(F) return -diff(F[1],y)+diff(F[2],x) end |
1 2 3 | F2 = [-x, -y] div(F2) rot(F2) |
\[ \begin{aligned}\left[ \begin{array}{r}- x\\- y\end{array} \right]\end{aligned} \]
\[ \begin{aligned}-2\end{aligned} \]
\[ \begin{aligned}0\end{aligned} \]
吸い込みがあり、回転のないベクトル場です。
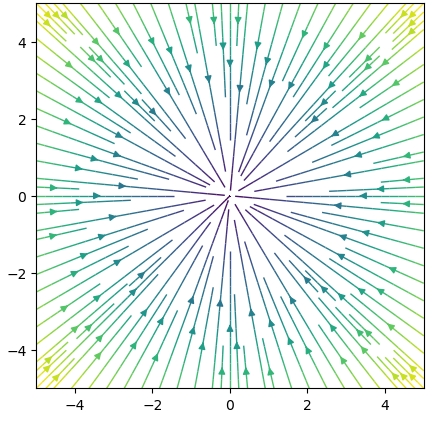
1 2 3 | F3 = [y, -x] div(F3) rot(F3) |
\[ \begin{aligned}\left[ \begin{array}{r}y\\- x\end{array} \right]\end{aligned} \]
\[ \begin{aligned}0\end{aligned} \]
\[ \begin{aligned}-2\end{aligned} \]
湧き出しや吸い込みがなく、回転があるベクトル場です。
合成関数の微分
\(g\)を2回微分可能な(一般的な)関数として、
\[ \begin{aligned}u(x,t):= g(x+ct)\end{aligned} \]
とするとき、\(u\)は波動方程式
\[ \begin{aligned}\frac{\partial^2 u }{\partial t^2} = c^2 \frac{\partial^2 u }{\partial x^2}\end{aligned} \]
を満たすことを確かめてみましょう。\(x,t \in \mathbb{R}\)で、\(c\)は定数です。
SymPyにおいて記号として扱える一般的な関数は、「sympy.Function(“g”)(x)」とします。
1 2 | g = sympy.Function("g")(x) u = g(x+c*t) |
\[ \begin{aligned}g(x)\end{aligned} \]
\[ \begin{aligned}g{\left(c t + x \right)}\end{aligned} \]
\(u\)を\(t,x\)の関数と見て、2回偏微分をそれぞれ計算してみましょう。
1 2 | diff(u,t,2) diff(u,x,2) |
\[ \begin{aligned}c^{2} \left. \frac{d^{2}}{d \xi_{1}^{2}} g{\left(\xi_{1} \right)} \right|_{\substack{ \xi_{1}=c t + x }}\end{aligned} \]
\[ \begin{aligned}\left. \frac{d^{2}}{d \xi_{1}^{2}} g{\left(\xi_{1} \right)} \right|_{\substack{ \xi_{1}=c t + x }}\end{aligned} \]
表示に出てくる\(\xi\)(クシー)は、\(g\)の変数です。\(\left. \frac{d^{2}}{d \xi_{1}^{2}} g{\left(\xi_{1} \right)} \right|_{\substack{ \xi_{1}=c t + x }}\)は、\(g\)を変数で2回(常)微分したあと、変数に\(ct+x\)を代入した値を意味しています。これはしばしば\(g^{\prime \prime}(ct+x)\)と略記されるものです。確かに、合成関数の微分がきちんと計算できていますね。
波動方程式を満たすかどうかチェックすると、
1 | diff(u,t,2) == c^2 * diff(u,x,2) |
1 | true |
きちんと満たしていることがわかります。
以上、Julia(SymPy)で偏微分、勾配、発散、回転、合成関数の微分を計算する方法を紹介してきました。
偏微分の具体的な計算は、高階になってくると複雑なので、コンピュータで計算できると嬉しいですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
Julia(Plotly)でグリグリ動かせる3Dグラフを作る方法
Julia(SymPy)でベクトルの計算をする方法(内積・ノルム・距離・角度、外積)
Julia(PyPlot)で2次元のベクトル場・流線を描く方法