どうも、木村(@kimu3_slime)です。
今回は、流体の複素ポテンシャル、速度ポテンシャル、流れ関数、流線とは何かを紹介します。
液体や気体のような流体の運動は、一般的にはナビエ・ストークスの方程式で説明されます。それは一般的には複雑なものなので、何かしらの仮定をつけて解くことが多いでしょう。
今回は、2次元の運動で、「渦なし(回転が0)」で「非圧縮(発散が0)」という条件を課すことにします。このとき、考えている領域には複素ポテンシャル(正則関数)
\[ \begin{aligned}F(z)= \Phi (x,y)+i \Psi (x,y)\end{aligned} \]
が存在し、その実部と虚部はラプラス方程式を満たすため、それによって流体の運動が記述できることが知られています。(証明について詳しくは「Advanced Engineering Mathematics」を参照してください)
より具体的に、第一象限\(D=\{z \mid x ,y > 0\}\)における複素ポテンシャル\(F(z)=z^2\)について考えましょう。
\(z= x+yi\)と直交座標で表すと、\(F(z)= (x+yi)^2 = x^2-y^2 +2xy i\)なので、\(\Phi (x,y)=x^2-y^2\)、\(\Psi (x,y)= 2xy\)です。
複素ポテンシャルの実部\(\Phi\)を速度ポテンシャル(velocity potential)、虚部\(\Psi \)は流れ関数(stream function)と呼びます。
さらに、\(\Phi \)の等高線を等ポテンシャル線(equipotential line)、\(\Psi\)の等高線を流線(streamline)、速度ポテンシャルの勾配\(V(x,y):= \nabla \Phi(x,y)\)を速度ベクトル(velocity vector)と呼びます。
これらを具体的に計算し、図示してみましょう。流線は、
\[ \begin{aligned}2xy =C\end{aligned} \]
なので、\(y = \frac{C}{2x}\)という双曲線になります。複素ポテンシャルの実部の等高線と虚部の等高線は直交するので、流線と直交する曲線が等ポテンシャルです。
また、速度ベクトルは\(V(x,y)= (2x,-2y)\)なので、\(D\)においては\(x\)軸の正の方向、\(y\)軸の負の方向へと流れています。これらを図示したのが、次の図です。
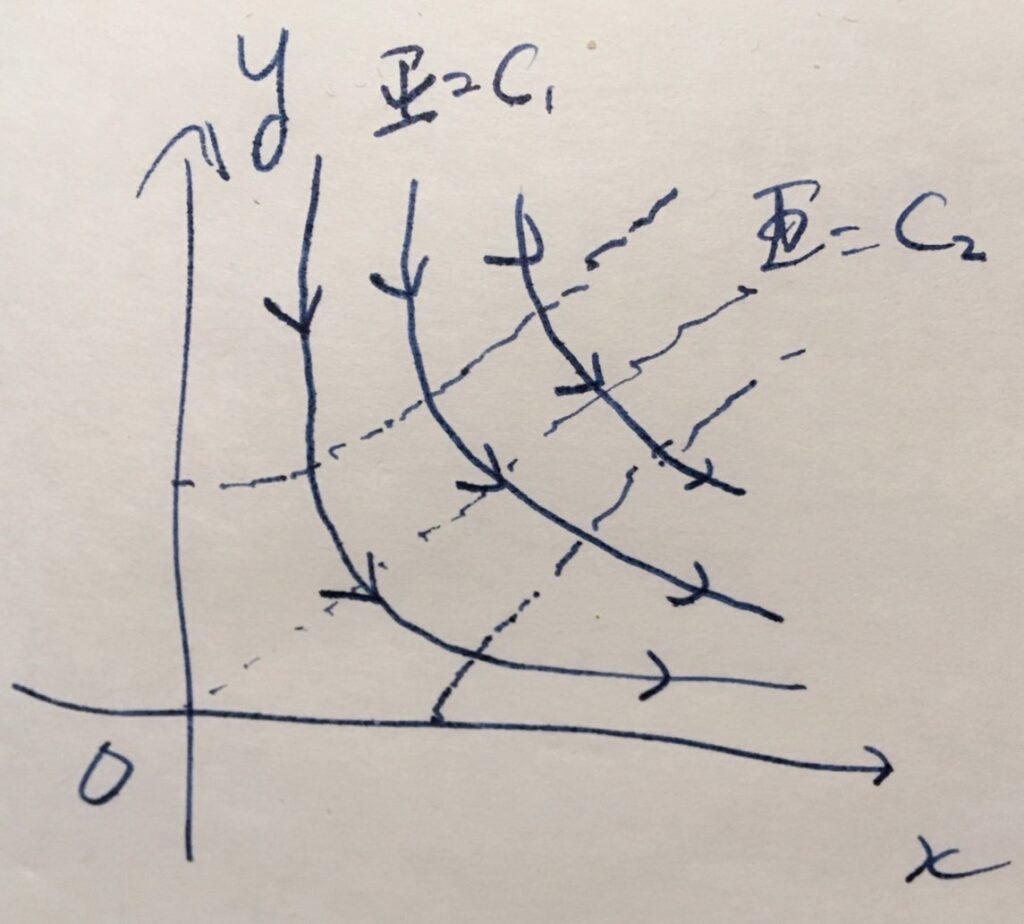
原点に角があって、そこで折れ曲がっているような流れです。速度は\(|V| =\sqrt{(2x)^2+(-2y)^2}= 2\sqrt{x^2+y^2}\)なので、原点からの距離が離れるほど速い流れとなっています。
速度ベクトルを複素の形式で表したとき、\(V(z):= \frac{\partial \Phi}{\partial x}+i \frac{\partial \Phi}{\partial y}\)を複素速度(complex velocity)と呼びます。これはコーシー・リーマンの方程式から、\(V(z)= \overline{F^{\prime }(z)}\)と表せることが知られています。
流線は、速度ベクトル\(V(x,y)= (2x,-2y)\)をベクトル場として図示して、それらをなめらかにつなげた曲線、とも言うことができます。
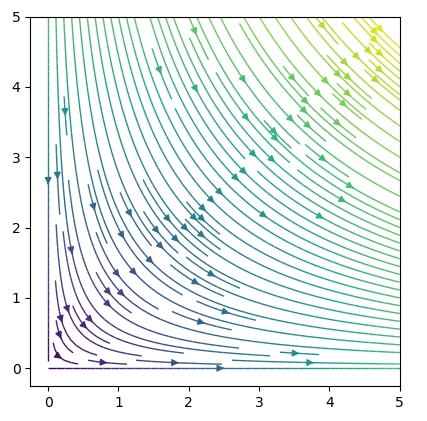
参考:ベクトル値関数をベクトル場として描いてみよう:ヤコビ行列と線形近似
以上、流体の複素ポテンシャル、速度ポテンシャル、流れ関数、流線とは何かを紹介してきました。
平面的な流体の運動の一部は、複素解析的な用語を使って説明できます。簡単な例ならば手書きでも図示できるので、試してみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
Kreyszig, E: Advanced Engineering Mathematics
Wiley John + Sons (2011-05-03T00:00:01Z)
¥10,314 (中古品)
岩波書店 (2003-12-12T00:00:01Z)
¥2,640
日本評論社 (2009-06-01T00:00:01Z)
¥5,170
東京大学出版会 (1985-04-25T00:00:01Z)
¥3,740
こちらもおすすめ
ベクトル値関数をベクトル場として描いてみよう:ヤコビ行列と線形近似