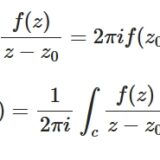どうも、木村(@kimu3_slime)です。
今回は、複素解析におけるリウビルの定理とは何か、例と証明を紹介します。
リウビルの定理
複素解析におけるリウビルの定理(Liouville’s theorem)とは、
という主張です。対偶として言い換えれば、「定数関数でない複素関数は、有界でないか、または複素数平面全体において正則でない」ということになります。
複素数平面\(\mathbb{C}\)全体において正則な関数は、整関数(entire function)と呼ばれることもあります。「有界な整関数は定数関数のみ」と言えば簡単です。
例えば、指数関数\(e^z\)は複素数全体で正則です。ただし、有界ではありません。実数直線上で\(\lim_{x\to \infty}e^{x}=\infty\)です。
三角関数は、実数直線上のみを考えれば有界です\(|\sin x|=1\)。定数関数でない例があるのは、考えている範囲を限定しているからです。複素数全体で\(\sin z\)は正則ですが、有界ではありません。オイラーの公式から\(\sin \theta = \frac{1}{2i}(e^{i\theta}-e^{-i\theta})\)なので、\(\theta = ai \)と虚軸方向を考えれば、\(a\to \infty\)で発散します。コサインについても同様です。
実数の世界で微分可能で有界な関数といえば、三角関数のように有界な関数もあります。しかし、「複素数全体では」と条件を強めれば、定数関数しかなくなってしまいます。広い範囲での微分可能性と有界性は、関数を制限する強い条件になっているわけですね。
有界かつ定数関数でない例としては、
\[ \begin{aligned}f(z)= \begin{cases}0 & (zの実部が負)\\1 & (zの実部が非負)\end{cases}\end{aligned} \]
といったものが考えられます。これは複素数全体で正則ではありません。例えば、\(z=0\)において連続でないので。
証明
では、リウビルの定理を証明しましょう。
\(f\)が有界なので、定数\(M\)で「すべての\(z\in \mathbb{C}\)に対し\(|f(z)|\leq M\)を満たす」ものが存在します。
\(f\)が複素数全体で正則かつ有界なので、コーシーの不等式から、任意の\(z \in \mathbb{C}\)、任意の\(r>0\)に対して
\[ \begin{aligned}|f^{\prime}(z)| \leq \frac{ M}{r}\end{aligned} \]
と評価できます。半径\(r\)を自由に選べるのが、複素数全体で正則という仮定の強さです。そこで\(r\to \infty\)とすると、
\[ \begin{aligned}f^{\prime}(z)=0\end{aligned} \]
です。
このとき、\(f\)が定数であることを、任意の\(z,w\)に対して\(f(z)=f(w)\)が成り立つことによって示しましょう。\(z,w\)をつなぐ直線を\(c\)とします。線積分の原始関数による計算(微積分学の基本定理)により、
\[ \begin{aligned}\int _c f^{\prime} dz = f(z)-f(w)\end{aligned} \]
です。一方、左辺は\(f^{\prime }(z)=0\)より0なので、\(f(z)=f(w)\)であること、\(f\)が定数関数であることが示せました。
証明のポイントは、コーシーの不等式によって、導関数の大きさが
\[ \begin{aligned}|f^{\prime}(z)| \leq \frac{ M}{r}\end{aligned} \]
と制限されることでしょう。広い範囲でコーシーの不等式を使えば、\(f^{\prime}\)の大きさは小さいと言わざるを得ない、実際には0になります。導関数がどこでも0になる関数は定数関数のみ、というのは納得できますね。
以上、複素解析におけるリウビルの定理とは何か、例と証明を紹介してきました。
リウビルの定理は、多項式は複素数の範囲で必ず解を持つ:代数学の基本定理の証明に利用することもできます。
複素関数、正則関数の特徴を知るために、リウビルの定理の主張を知っておくと良いでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
Kreyszig, E: Advanced Engineering Mathematics
Wiley John + Sons (2011-05-03T00:00:01Z)
¥10,314 (中古品)
岩波書店 (2003-12-12T00:00:01Z)
¥2,640
日本評論社 (2009-06-01T00:00:01Z)
¥5,170
東京大学出版会 (1985-04-25T00:00:01Z)
¥3,740
こちらもおすすめ
上限・下限(sup,inf)、有界とは:具体例、最大・最小値との違い
オイラーの公式、極形式、ド・モアブルの定理とは:複素指数関数、三角関数の性質
コーシーの積分公式とは、計算例と応用(無限回微分可能、コーシーの不等式)