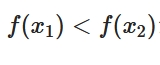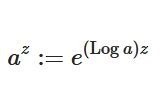複素対数関数の主値Log zとは、計算例

どうも、木村（@kimu3_slime）です。

今回は、複素関数の対数関数\(\mathrm{Log\,} z\)、主値とは何かを紹介します。

前提知識：複素関数の主値、多価関数・一価関数とは：平方根、ルートを例に

複素対数関数、主値とは

実変数の対数関数\(\log x\)は、指数関数\(e^{x}\)の逆関数でした。

実数を変数とする指数関数は単調増加なので、逆関数を持ちます。その逆関数が対数関数というわけです。

さて、複素変数の対数関数\(\log z\)はどのように捉えたら良いでしょうか？

複素指数関数\(e^{z}\)の逆関数として捉えたいわけですが、そこには単調性もなく、逆関数を素朴には与えることができません。

例として、\(e^z =1\)という方程式を考えましょう。もし、\(z\)を実数に限定するならば、その解はただひとつ\(z=0\)で、逆像として\(\log 1=0\)が定まります。

しかし、\(z\)が複素数の場合は、\(e^{z}=1\)の解はひとつではありません。オイラーの公式により、\(z= a+bi\)とすると、\(e^{z}= e^{a}(\cos b + i \sin b )=1\)です。両辺の大きさを比較すると、\(a=0\)は定まります。しかし偏角を比較すれば、\(\cos b =1\)が得られ、\(b= 2k\pi\),\(k\)は整数が解です。\(z=0,2\pi i,-2\pi i,4\pi i\)と、無限に解があります。このままでは対数関数が多価関数となってしまい、一価の関数として定めることができません。そこで、\(z=0\)のケースを選ぶように値域に制限をかけるのが、主値を考える、という議論になります。

今までの議論を一般化しましょう。

\(w= \log z\)という関数を定義したいとします。それは、\(e^{w}=z\)という逆関数の関係を満たしていてほしいです。

変数を\(w= a+bi\)、\(z=re^{i \theta}\)（極形式）と表しましょう。方程式は、\(e^{a}e^{bi}= re^{i\theta}\)となります。両辺の絶対値を比較すれば、\(e^{a}= r\)です。偏角を比較すると、\(b = \theta + 2k\pi \)、\(k\)は整数です（複素数の偏角は、\(2\pi\)の定数倍の分だけの不定性があることに注意）。

この結果を\(w= \log z\)の形に戻しましょう。\(e^{a}=r=|z|\)から、\(a = \log _e |z|\)です（この\(\log\)は実変数の対数関数で、既知のもの）。したがって、

\[ \begin{aligned}\log z = \log |z| + (\theta+2k\pi) i \end{aligned} \]

となりました。ただし、このままでは\(k\)によって複数の値を取ることになってしまいます。そこで、\(k=0\)のケースとして、対数関数の主値を選びましょう。

\[ \begin{aligned}\mathrm{Log\,} z := \log |z| + \theta i\end{aligned} \]

と書きます。これを複素対数関数の主値と呼びます。Lを大文字にしているのは、主値を取っていることを強調したものです。主値のケースでも単に\(\log z\)と表記されることもあります。

\(k=0\)のケースとは、\(- \pi < \theta \leq \pi\)を考えることとします。これは偏角の主値\(- \pi < \mathrm{Arg\,} z \leq \pi\)を選ぶことに対応しています。

画像引用：Log[z] – WolframAlpha

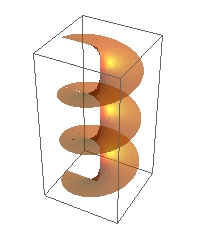
複素対数関数をグラフにしたのが、上の図です。ただし、主値だけでなく、複数の値（分枝）もセットでつなぎ合わせて描いたものとなっています（リーマン面）。上の図では、特定の複素数値に対し複数の値を持つことになるので、その一部を取りだしたのが主値のイメージです。

例として、\(\mathrm{Log\,} i\)を求めてみましょう。\(i\)の絶対値は\(1\)、偏角の主値は\(\frac{\pi}{2}\)です。

したがって、複素対数関数の定義から、

\[ \begin{aligned}\mathrm{Log\,}{i} = \log 1 + (\frac{\pi}{2}) i \\ = \frac{\pi}{2}i\end{aligned} \]

と求められました。

\(e^{z}=i\)の解自体は、\(\frac{\pi}{2}i\)だけでなく、\(\frac{\pi}{2}i +2k\pi i\)といったものが解です。対数関数の主値は、その中から\(\frac{\pi}{2}i\)を取り出したものとなっています。

複素対数関数は、今までの議論から、\(e^{\mathrm{Log\, } z}=z\)を満たしています。しかし、\(\mathrm{Log\, } e^z=z\)は一般に成り立たないことに注意しましょう。複素対数関数の主値の値域は、虚部の大きさが\(- \pi < \theta \leq \pi\)です。\(z\)がその外側の値としたら、成り立ちません。例えば、\(z= \frac{\pi}{2}i+2\pi i\)とすると、\(\mathrm{Log\, } e^z = \frac{\pi}{2}i\)なので等しくありませんね。したがって、「\(e^{z}=e^{w}\)だから両辺の対数を取って\(z=w\)」とは一般には議論できないことに注意しましょう。

複素対数関数は、\(z=0\)と実軸の負の部分を除いて複素微分可能（正則）であることが知られています（コーシー・リーマンの方程式を満たすことが示せる）。

\[ \begin{aligned}(\mathrm{Log\,})^\prime = \frac{1}{z}\end{aligned} \]

以上、複素関数の対数関数\(\mathrm{Log\,} z\)、主値とは何かを紹介してきました。

僕は複素解析を学び初めの頃、対数の主値の考え方がイマイチ理解できませんでした。それは例えば、実数のケースと異なり、\(e^{z}=1\)のような方程式が無限に解を持つことを認識していなかったからだと思います。

複素指数関数、オイラーの公式を考えれば、虚部の方向には周期的であることがわかります。それを踏まえれば、複素対数関数の主値を考える意義や、計算も理解できるようになるでしょう。

木村すらいむ（@kimu3_slime）でした。ではでは。