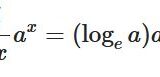数学の問題で試行錯誤ができないときの対処法：ゴールを自分で決める

どうも、木村（@kimu3_slime）です。

「数学の簡単な問題の多くは、試行錯誤によって解けることがある。なのに、どうして何もできずに解けない人がいるのだろう」。と、中学や高校のときに僕は思っていました。

しかしよく考えてみると、試行錯誤の考え方ややり方について、学校で教わった記憶はあまりないのです。今回は、試行錯誤の前提となる僕なりの考え方を紹介します。

謎解きゲームが苦手な人のプレイを見て気づいたこと。
「何をすればクリアになるのか」という目的意識がない。ウロウロと「探索」したところで、目的を仮にでも設定しなければ、解法もヒントも見つかりようがない。
仮説や目的がないと、時間をかけても悲しいことに試行錯誤にすらならない、と思った。
— 木村すらいむ (@kimu3_slime) October 15, 2021

ゴールを自分で決める

「\(12\times 34\)を計算せよ」という問題の解き方がわからない人は、中学生ならほぼいないでしょう。たとえ掛け算や筆算のやり方を忘れてしまったとしても、その「やり方を使えば解ける」という解き方は思いつくはずです。

なぜなら、「掛け算を計算せよ」という形の問題は、「掛け算によって解きなさい」という回答方針（How）が明確だからです。

しかし、もう少し難しい問題になると、回答方針が立たず、何から手をつければ良いかわからなくなってしまうかもしれません。例えば、

\[ \begin{aligned}a_{n+1}=n a_{n}\\ a_1 =1\end{aligned} \]

を満たす数列\(a_n\)を求めよ

という問題ならどうでしょうか。僕ならば、次のように考えて解きます。

示すべきこと：\(a_n\)を\(n\)を使って表し、漸化式の条件を満たすことを確かめる

そのために：\(a_n\)の表示式を予想する。

既存の解き方を調べる：問題の漸化式は、等差数列でも、等比数列でもない。

既存の解き方が使えないので、試行錯誤する。つまり、\(n=1,2,3,\dots\)のケースを考えてみる。すると、\(a_2 =2\)、\(a_3 =6\)、\(a_4 =24\)とわかる。

（階乗の知識を持っているので）この関係性から、\(a_n =n !\)と予想される。これは実際、漸化式を満たす（証明は略）。

まず、「示すべきことはなにか？、ゴールは何か？（What）」と必ず考えます。入り組んだ問題ならば、わかりやすく大きく文字で書き出すことさえあります。これさえできれば、問題は解ける。そういう目標や条件を意識します。

続いて、その目標を達成するための手段（How）を考えます。上の例ならば、「\(a_n\)の形を予想する」手段を考えるのです。教科書で学んだ知識から、漸化式が等差数列または等比数列に当てはまるならば、解くことができます（形から係数を決めても良いし、公式を当てはめても良い）。

今回は、既存の知識に手段が当てはまらなかったので、より原始的な方法、\(n\)が小さいときの値を知り、試行錯誤で形を見出しました。確率や漸化式の問題は、この手の試行錯誤や数学的帰納法は有効です。

今回の問題をもう少し簡単にするならば、

(1) \(a_2,a_3\)の値を求めよ

や

「\(a_n= n!\)が漸化式を満たすことを示せ」

といった誘導をつけるでしょう。ここまで来ると、「何をすべきか」と考える必要すらなく、「どうやって解くか、代入して確かめれば良い」と解ける人は増えるはずです。しかし、それだと中級レベルの問題が解けません。

そこで「試行錯誤すれば良い」と僕はかつて思っていたのですが、それには前提があるなと気づきました。

そもそも、解くべき問題は何か、何を答えれば答えになるかを明確に意識すること。簡単な問題なら「どうやって解くか」だけを考えれば解けるのですが、難しい問題になるほど「そもそも何をすれば良いのか」が見つけにくくなっていきます。

たとえ話として、探索しながら解くパズルゲームや脱出ゲームの解き方を考えてみましょう。目標を設定せず、手当たりしだいに探索しているだけでは、（偶然を除き）めったに問題を解くことはできないでしょう。たとえゲーム内で明確にそう示されていなかったとしても、「次に解くべきはこの小問題だろう」と仮説を立て、その問題を解くための方法を探す。そういう探索ならば、答えは見つかっていきます。

つまり、「何をすればクリアになるのか」と考えながら探索するのが意味ある試行錯誤であって、目的を持たずに闇雲に歩き回っても、疲れるだけで答えは見つからないと思います。

数学の勉強や問題の解き方も同じだと思います。学校の授業では、しばしば「どうやって解くか（How）」が重視されがちです。問題がHowと結びつきやすい簡単な問題ならば、そのHowを当てはめるだけで解けるでしょう。しかしちょっと難しくなれば、「何をすべきか（What）」を考え、そのための手段（How）を考えなかれば解けなくなってきます。

何をすれば答えになるか目標設定する、その意志を持って初めて、知識や公式を当てはめたり、試行錯誤という手段が生まれてくるわけですね。

以上、数学の問題で試行錯誤ができないときの対処法として、ゴールを自分で決めることの大切さについて書いてきました。

もう少し具体的な問題の解き方の話は、次の記事で紹介しています。

参考：手の付け方がわからない数学の問題の解き方：定義を確認し、単純化しよう

目標や仮説を持って課題に取り掛かるという考え方は、数学に限らなず、問題解決全般において大事だと思うので、ぜひ試してみてはいかがでしょうか。

木村すらいむ（@kimu3_slime）でした。ではでは。