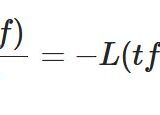ラゲールの方程式、多項式とは：ラプラス変換による解法

どうも、木村（@kimu3_slime）です。

今回は、ラゲールの方程式、多項式とは何か、そのラプラス変換による解法を紹介します。

ラゲールの方程式（Laguerre’s equation）とは、

\[ \begin{aligned}x y^{\prime \prime}+(1-x)y^{\prime}+ny=0\end{aligned} \]

と表される微分方程式です。非負の整数\(n\)をパラメータとしています。

この方程式は、水素原子に関するシュレーディンガー方程式の同径方向の解を得る中で登場することが知られています。

では、ラプラス変換によって方程式を解いてみましょう。

今回は\(x\)が係数として登場する変数係数の方程式なので、ラプラス変換の微分を利用します。

\[ \begin{aligned} & L(xy^{\prime})\\ &= -L(y)-s\frac{dL(y)}{ds}\end{aligned} \]

\[ \begin{aligned} & L(xy^{\prime\prime}) \\ &= -2sL(y)-s^2\frac{dL(y)}{ds}+y(0)\end{aligned} \]

なので、これを使って方程式をラプラス変換すれば

\[ \begin{aligned}-2sL(y)-s^2\frac{dL(y)}{ds}+y(0) \\+ sL(y)-y(0)\\-(-L(y)-s\frac{dL(y)}{ds})+nL(y)\\ =0\end{aligned} \]

\[ \begin{aligned}(s-s^2)\frac{dL(y)}{ds}+(n+1-s)L(y)=0\end{aligned} \]

\[ \begin{aligned} \frac{1}{L(y)}\frac{dL(y)}{ds} &= -\frac{n+1-s}{s-s^2}\\ &= \frac{1}{s-1}-\frac{n+1}{s}\end{aligned} \]

となります。これは変数分離形なので、両辺を\(s\)について積分すれば

\[ \begin{aligned}\log (L(y)) = n \log (s-1)-(n+1)\log s+C\end{aligned} \]

\[ \begin{aligned}L(y) = C_1 \frac{(s-1)^n}{s^{n+1}}\end{aligned} \]

となりました。

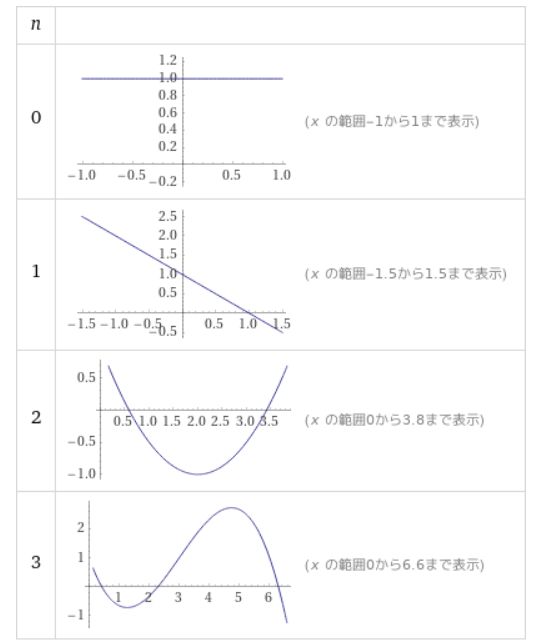
以降、特に\(C_1=1\)とするケースを考え、逆変換して得られる解\(y_n\)を求めましょう。

\(n=0\)のときは、\(L(y)=\frac{1}{s}\)なので、逆変換は定数\(y_0 (x)=1\)です。

\(n=1\)のとき、\(L(y)= \frac{s-1}{s^2}\)です。\(s-1\)が出てきているので、第一シフト定理と\(L(x) =\frac{1}{s^2} \)を使うと、\(L(xe^{-x}) = \frac{1}{(s+1)^2}\)となります。これに\(s\)がかかってほしいので、微分のラプラス変換を使えば、

\[ \begin{aligned} L(\frac{d}{dx} (xe^{-x})) &=s L(xe^{-x}) \\ &= \frac{s}{(s+1)^2}\end{aligned} \]

です。よって、第一シフト定理から

\[ \begin{aligned}y_1(x) = e^{x}\frac{d}{dx} (xe^{-x})\end{aligned} \]

と解が得られました。

一般の\(n\)についても同様に求められます。微分のラプラス変換を使えば、

\[ \begin{aligned}L(x^n) = \frac{n!}{s^{n+1}}\end{aligned} \]

\[ \begin{aligned}L(x^n e^{-x}) =\frac{n!}{(s+1)^{n+1}}\end{aligned} \]

\[ \begin{aligned}L(\frac{d^n}{dx^n} (x^n e^{-x}))=\frac{n! s^n}{(s+1)^{n+1}}\end{aligned} \]

より、解は

\[ \begin{aligned}y_n(x) = \frac{e^{x}}{n!}\frac{d^n}{dx^n} (x^n e^{-x})\end{aligned} \]

と求められました。

これは\(e^{x}\)についてはキャンセルされ\(x\)に関する多項式となり、ラゲールの多項式（Laguerre’s polynomial）と呼ばれています。特に微分を使ったこの表示式は、ロドリゲスの公式（Rodrigues’s formula）と呼ばれるものです。