どうも、木村(@kimu3_slime)です。
今回は、バネの振動(単振動)の運動方程式、微分方程式の解き方を紹介します。
次の図に示されるような運動を考えましょう。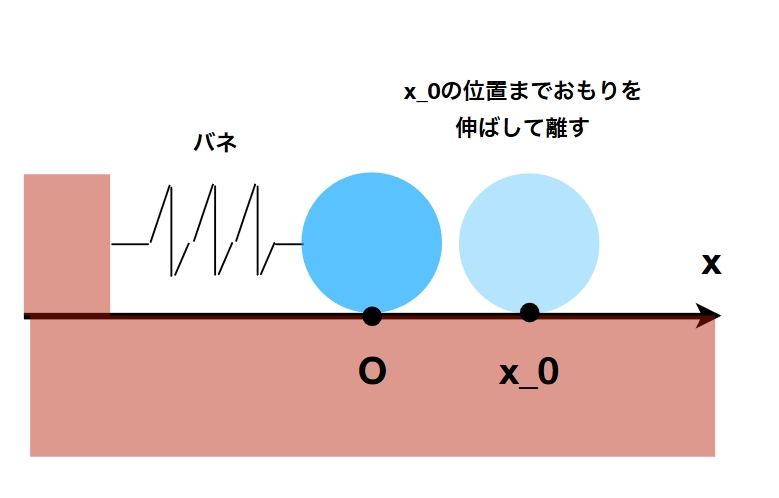
バネの自然長(何も力を加えていないときの長さ)を基準とし、おもりの位置(変位)を\(x(t)\)と表すことにします。おもりの質量を\(m\)とすると、運動方程式は
\[ \begin{aligned}m\frac{d^2x}{dt^2}= -kx\end{aligned} \]
と表されます。
\(k>0\)はばね定数と呼ばれる定数で、バネによる力がこのように表されるのはフックの法則と呼ばれるものです。
さて、この微分方程式を解いてみましょう。これは\(x\)に関する2階の線形微分方程式です。
解き方:2階線形常微分方程式の解き方、学ぶ意味:熱方程式への応用を例に、線形微分方程式はなぜ指数関数e^{λt}と仮定して解いて良いか
まず、微分方程式
\[ \begin{aligned}\frac{d^2x}{dt^2}= -\frac{k}{m}x\end{aligned} \]
に対応する特性方程式は
\[ \begin{aligned} \lambda ^2 =-\frac{k}{m}\end{aligned} \]
です。これを解くと、\(\lambda = \pm \sqrt{\frac{k}{m}} i\)となります。
複素共役な解のときは、2階線形微分方程式の解は、実部\(0\)と虚部\(\sqrt{\frac{k}{m}}\)を使って
\[ \begin{aligned} x(t) &= e^{0t}(C_1 \cos( \sqrt{\frac{k}{m}} t)+C_2 \sin( \sqrt{\frac{k}{m}} t)) \\ &= C_1 \cos( \sqrt{\frac{k}{m}} t)+C_2 (\sin \sqrt{\frac{k}{m}} t))\end{aligned} \]
と表せます。さらに、初期条件を\(x(0)=x_0\)、\(\frac{dx}{dt}(0)=v_0\)とすれば、
\[ \begin{aligned} x(t) = x_0 \cos( \sqrt{\frac{k}{m}} t)+v_0 \sin (\sqrt{\frac{k}{m}} t) \end{aligned} \]
と微分方程式を解くことができました。(実際に微分すれば、これが解であることを確かめることもできます)
特に、おもりを静かに離す(\(v_0 =0\))ときは、
\[ \begin{aligned} x(t) = x_0 \cos( \sqrt{\frac{k}{m}} t) \end{aligned} \]
とコサインのみで表せます。バネのように周期的な運動が表せていますね。
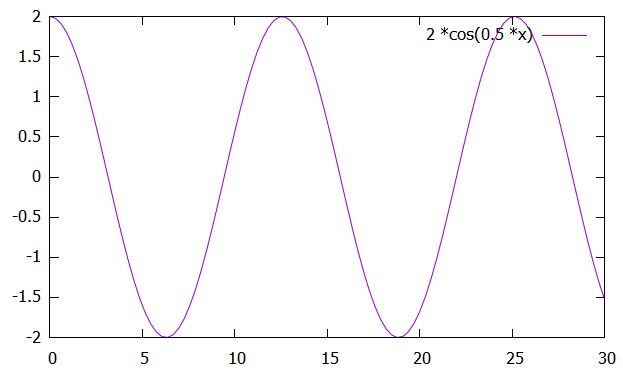
このバネによる運動は、単振動(simple harmonic motion)、調和振動(harmonic oscillator)と呼ばれるものです。
参考:サイン、コサインは何の役に立つ? バネの振動と三角関数
その振幅は、初期位置\(x_0\)ですね。また、周期\(T\)は、コサインの中身を見れば\(\sqrt{\frac{k}{m}} T = 2\pi \)を満たすので、\(T =2\pi \sqrt{\frac{m}{k}}\)となります。
角振動数(角速度)\(\omega\)は
\[ \begin{aligned}\omega :=\frac{2\pi}{T}= \sqrt{\frac{k}{m}} \end{aligned} \]
です。\(m,k\)の代わりに\(\omega\)を使って方程式と解を表すと、
\[ \begin{aligned}\frac{d^2x}{dt^2}= -\omega^2 x\end{aligned} \]
\[ \begin{aligned} x(t) = x_0 \cos( \omega t)+v_0 \sin ( \omega t) \end{aligned} \]
とシンプルに表せます。
エネルギーについて考えましょう。運動方程式
\[ \begin{aligned}m\frac{d^2x}{dt^2}= -kx\end{aligned} \]
の両辺に\(v= \frac{dx}{dt}\)をかけて、\(0\)から\(t\)まで積分しましょう。
\[ \begin{aligned}\frac{d}{dt}(\frac{1}{2} mv^2) =m\frac{d^2x}{dt^2} \frac{dx}{dt} \end{aligned} \]
\[ \begin{aligned}\frac{d}{dt}(-\frac{1}{2} kx^2) = -kx \frac{dx}{dt}\end{aligned} \]
となるので、
\[ \begin{aligned} \frac{1}{2} mv^2 -\frac{1}{2} mv_0^2 = -\frac{1}{2}kx^2 +\frac{1}{2}kx_0^2\end{aligned} \]
\[ \begin{aligned} \frac{1}{2} mv(t)^2+\frac{1}{2}kx(t)^2 =\frac{1}{2} mv_0^2 +\frac{1}{2}kx_0^2\end{aligned} \]
です。
運動エネルギー\(K=\frac{1}{2}m v^2\)とバネによる位置エネルギー(弾性エネルギー)\(U=\frac{1}{2}kx^2 \)の和が、時間が経っても一定である、力学的エネルギーが保存されることがわかりました。特に、
以上、バネの運動:単振動の運動方程式、微分方程式の解き方を紹介してきました。
特性方程式は複素共役解が表れ、解には三角関数が表れます。摩擦・減衰のあるバネの運動、振り子の運動を考える上でも、まずは摩擦なしのバネの運動を知っておくと良いでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
Pearson (2016-03-02T00:00:00.000Z)
¥4,910
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥6,333 (中古品)
朝倉書店 (2002-01-01T00:00:01Z)
¥2,215 (中古品)
こちらもおすすめ
2階線形常微分方程式の解き方、学ぶ意味:熱方程式への応用を例に
線形微分方程式はなぜ指数関数e^{λt}と仮定して解いて良いか