関数の連続（極限）と数列連続（点列連続）の定義が同値であることの証明

どうも、木村（@kimu3_slime）です。

今回は、関数の極限による連続性と数列連続（点列連続）の定義が同値であることの証明を紹介します。

連続性の2種の定義は同値

\(f:I \to \mathbb{R}\)を区間\(I\)で定義された関数としましょう。

\(f\)が点\(a \in I\)において連続である（continuous）とは、\(\lim_{x \to a }f(x)=f(a)\)が成り立つことです。

論理記号を使って言えば、

\[ \begin{aligned}(\forall \varepsilon >0 )(\exists \delta >0)(\forall x \in \mathbb{R})\\(|x-a|< \delta \Rightarrow |f(x)-f(a)|<\varepsilon)\end{aligned} \]

と言えます。

一方、\(f\)が点\(a \in I\)において数列連続（点列連続）である（sequentially continuous）とは、任意の\(I\)の点列\((x_n)_{n\in\mathbb{N}}\)で\(a\)に収束するようなものを考えると、\(\lim_{n\to \infty} f(x_n)=f(a)\)が成り立つことです。

点列の極限\(\lim_{n\to \infty}x_n =a\)の定義を論理記号を使って書くと、

\[ \begin{aligned}(\forall \varepsilon >0 )(\exists N \in \mathbb{N})(\forall n \in \mathbb{N})\\(n \geq N \Rightarrow |x_n-a|<\varepsilon)\end{aligned} \]

となります。

教科書によっては、後者の定義も単に関数が「連続である」ことの定義として書かれていたりします。

微積分学を学びはじめの頃の僕は、どれが連続であることの定義なのだと混乱していましたが、これらの定義は同値です。

\(I\)を開区間、\(a \in I\)とする。次の条件は同値。

\(f\)が\(a\)において連続である
\(f\)が\(a\)において点列連続である

これを証明してみましょう。

まず、1を仮定します。\((x_n)_{n \in \mathbb{N}}\)を\(a\)に収束する任意の点列としましょう。示したいことは、\(\lim_{n\to \infty} f(x_n)=f(a)\)です。

任意に\(\varepsilon >0\)を選びます。\(\lim _{x\to a}f(x)=f(a)\)より、「\(|x-a| <\delta \)ならば\(|f(x)-f(a)|< \delta\)」を満たす\(\delta >0\)が存在します。この\(\delta\)を使って、\(\lim_{n \to \infty}x_n =a\)より、「すべての自然数\(n \in \mathbb{N}\)に対し、\( n \geq N\)ならば\(|x_n -a|< \delta\)」を満たすような\(N \in \mathbb{N}\)が存在します。\(|x_n-a |<\delta \)が満たされるので、\(|f(x_n)- f(a)|<\delta\)です。まとめると、「すべての自然数\(n \in \mathbb{N}\)に対し、\( n \geq N\)ならば\(|f(x_n) -a|< \delta\)」を満たすような\(N \in \mathbb{N}\)が存在が言えました。つまり2が言えました。

一方で、2ならば1を示すために、その対偶を示しましょう。\(f\)が\(a\)で連続でないと仮定し、\(\lim_{n\to \infty}x_n =a\)であるが、\(\lim_{n \to \infty}f(x_n)=f(a)\)を満たさない数列\((x_n)\)が存在することを示します。連続であることの否定は、

\[ \begin{aligned}(\exists \varepsilon >0 )(\forall \delta >0)(\exists x \in \mathbb{R})\\(|x-a|< \delta かつ |f(x)-f(a)| \geq \varepsilon)\end{aligned} \]

です。\(\varepsilon>0\)を条件を満たすものとします。例えば\(\delta =\frac{1}{n}\)（\(n\)は自然数）のケースを考えると、それぞれの\(n\)に対して、連続でないことから\(x_n \in \mathbb{R}\)で「\(|x_n-a|<\frac{1}{n}\)かつ\(|f(x_n)-f(a)| \geq \varepsilon\)」を満たすようなものが存在します。\(|x_n-a|<\frac{1}{n}\)であり、\(\lim _{n \to \infty} \frac{1}{n}=0\)なので、はさみうちの原理より\(\lim_{n \to \infty}x_n =a\)です。一方、\(f(x_n)\)は\(f(a)\)に収束しません。ある\(\varepsilon>0\)で、次の条件を満たすものが存在しているからです。すべての\(n \in \mathbb{N}\)に対し、\(|f(x_n)-f(a)| \geq \varepsilon\)を満たす（\(N=1\)と考えている）。よって、\(f\)は\(a\)で点列連続でないことが示せました。

以上の議論は、特に実数\(\mathbb{R}\)特有の話を利用していません。\(N\)次元のユークリッド空間\(\mathbb{R}^N\)、一般に距離空間において、関数（写像）の連続性と点列連続性が同値であることが示せます。

考えている開区間\(I\)は開集合として一般化すれば良いです。連続性の定義に表れる\(|x-a|< \delta\)といった表現は、ノルムを使えば\(\|x-a\|<\delta\)、距離を使えば\(d(x,a)<\delta\)と表せます。

今回の話を利用すれば、関数が連続でないことを示すには、ひとつでも都合の悪い点列を見つければ良い、ということになります。

平面\(\mathbb{R}^2\)における実数値関数\(f\)

\[ \begin{aligned}f(x,y)= \begin{cases} \frac{xy}{x^2+y^2} & ((x,y) \neq (0,0) )\\0& ((x,y)=0)\end{cases}\end{aligned} \]

が、\(a=(0,0)\)で不連続であることを示しましょう。平面におけるこの手の関数の連続性を調べるには、\(x=r\cos \theta, y =r \sin \theta\)という極座標表示が役立ちます。それを使うと、\((x,y) \neq (0,0)\)のときは、\(f(x,y)=\frac{r^2 \sin \theta \cos \theta}{r^2}= \sin \theta \cos \theta\)となっています。例えば\(\theta =\frac{\pi}{4}\)とすれば、\(\sin \theta = \cos \theta = \frac{\sqrt{2}}{2}\)です。この角度から原点に近づくと、どんなに近づいても値が0でなく一定のまま、というわけです。

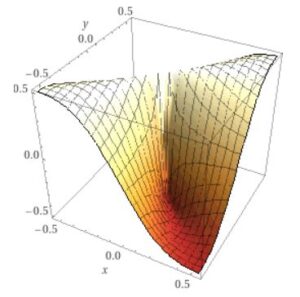
画像引用：WolframAlpha

これを利用して、\((x_n,y_n)= (\frac{1}{n} \cos \frac{\pi}{4}, \frac{1}{n} \sin \frac{\pi}{4})\)という点列を考えましょう。この点列は、\(\lim_{n\to \infty}(x_n,y_n)=(0,0)\)を満たします。しかし、\(\lim_{n\to \infty}f(x_n,y_n)= \cos\frac{\pi}{4} \sin \frac{\pi}{4} =\frac{1}{2}\)で、\(f(0,0)=0\)に収束しません。点列連続と連続の同値性から、\(f\)の非連続性が言えました。

以上、関数の連続（極限）と数列連続（点列連続）の定義が同値であることの証明を紹介してきました。

イプシロンデルタ的な話は最初のうちは難しいかも知れませんが、このように2つの似た定義が同値であることを説明するのに役立っています。連続性について考えるときは、連続的な極限を考えても、点列的な極限を考えてもどちらでも良い、と安心してもらえたら嬉しいです。

木村すらいむ（@kimu3_slime）でした。ではでは。