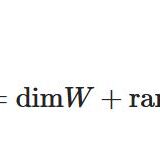線形写像の核、像の定義：部分空間となることの証明

どうも、木村（@kimu3_slime）です。

今回は、線形写像の核、像の定義、それが部分空間となることの証明を紹介します。

線形写像、像、核、部分空間とは
核が部分空間となること
像が部分空間となること

こちらもおすすめ

線形写像、像、核、部分空間とは

まず、言葉の定義を確認しておきましょう。

\(V,W\)を線形空間とする。写像\(f:V\to W\)が

(1) 加法性：任意の\(x,y \in V\)に対し、\(f(x+y)= f(x)+f(y)\)

(2) 斉次性：任意の数\(c\)に対し、\(f(cx) =cf(x)\)

を満たすとき、\(f\)は線形写像と呼ぶ。（(1),(2)の条件は、合わせて線形性と呼ばれる）

参考：線形写像かどうか調べる方法をわかりやすく解説

\(A\)を行列として、\(f(x):=Ax\)により\(f\)を定めると、\(f\)は線形写像です。つまりこれからする議論は、\(f\)を行列に置き換えても当てはまるものです。

線形写像\(f\)の核と像は、

\[ \begin{aligned}\ker f :=\{ x\in V \mid f(x) =0\}\end{aligned} \]

\[ \begin{aligned} f(V) :=\{ y\in W \mid ある x \in V によって y=f(x) と表せる\}\end{aligned} \]

と定義されます。

\(f\)が行列であるとき、その核は線形方程式の解空間です。その像は、行列の列ベクトルが生成する空間と言えます。

線形空間\(X\)の部分集合\(Y\)が部分空間であるとは、

\(X\)の演算について、\(Y\)が閉じている
1. 和について閉じている：\(x,y \in Y\)ならば、\(x+y \in Y\)
2. スカラー倍について閉じている：\(x \in Y\)、\(a\)をスカラーとするなら、\( ax \in Y\)

を満たすことです。

核が部分空間となること

線形写像の核

\[ \begin{aligned}\ker f :=\{ x\in V \mid f(x) =0\}\end{aligned} \]

は、\(V\)の部分集合です。これが\(V\)の部分空間であることを示しましょう。

和について：\(x,y \in \ker f\)とすると、核の定義から\(f(x)=0,f(y)=0\)が成り立ちます。\(f\)は線形写像なので、\(f(x+y)=f(x)+f(y)=0\)です。よって、\(x+y \in \ker f\)です。

スカラー倍について：\(x \in \ker f\)、\(a \)をスカラーとします。\(f\)は線形写像なので、\(f(ax)=af(x)=a0 =0\)です。よって、\(ax \in \ker f\)です。

以上により、\(\ker f\)は部分空間です。

像が部分空間となること

\(f\)の像

\[ \begin{aligned} f(V) :=\{ y\in W \mid ある x \in V によって y=f(x) と表せる\}\end{aligned} \]

は、\(W\)の部分集合です。これが\(W\)の部分空間であることを示しましょう。

和について：\(x,y \in f(V)\)とすると、像の定義から\(f(z)=x,f(w)=y\)を満たす\(z,w \in V\)が存在します。\(f\)は線形写像なので、\(f(z+w)=f(z)+f(w)= x+y\)が成り立ちます。\(z+w \in V\)を\(f\)で写した像として表せたので、\(x+y \in f(V)\)です。

スカラー倍について：\(x \in f(V)\)、\(a \)をスカラーとします。像の定義から\(f(z)= x\)を満たす\(z\in V\)が存在します。\(f\)は線形写像なので、\(f(az)=af(z) =ax\)です。\(az \in V\)なので、像の定義から\(ax \in f(V)\)となります。

以上によって、\(f(V)\)は部分空間です。

線形写像の核、像が部分空間となることの証明を紹介してきました。これは単に行列に限らず、一般的な線形空間、線形写像について成り立つ性質です。\(f\)が線形写像でなくなると、核や像は部分空間とは限らなくなります（例を考えてみてください）。

ちなみに、核の次元\(\mathrm{dim}(\ker f)\)を退化次数、像の次元\(\mathrm{dim}( f(V))\)を\(f\)のランクと呼びます。退化次数とランクについては、次元定理という強力な性質が成り立つことが知られています。

線形写像、その核と像の話は一般論でありながら扱いやすいので、ぜひその定義や証明を何も見ずに書けるようになってみてください。

木村すらいむ（@kimu3_slime）でした。ではでは。