どうも、木村(@kimu3_slime)です。
高校数学では、ある数の2分の1乗、分数乗といった考え方が登場します。
「2分の1回かけるってどういうこと?」と疑問に思う人向けに、2分の1乗、分数乗とは何か、どうしてそう考えるか(指数法則)を紹介していきます。
べき乗のべき乗の性質
まずは、わかりやすいプラスのべき乗の性質を調べていきましょう。例えば2の3乗\(2^3\)とは、
\[ \begin{aligned}2^3 := 2\times 2\times 2\end{aligned} \]
と3回かけることで定義されています。これをさらに2乗してみましょう。すると、
\[ \begin{aligned}(2^3)^2 = (2\times 2\times 2)(2\times 2\times 2)=2^6\end{aligned} \]
となり、\((2^3 )^2 =2^{2\times 3}=2 ^6\)が成り立っています。
一般には、\(n\)乗した数をさらに\(m\)乗すると、合計で\(n\times m\)回その数をかけることになるので、
\[ \begin{aligned}(2^{n})^m =2^{n\times m}\end{aligned} \]
\[ \begin{aligned}(a^{n})^m =a^{n\times m}\end{aligned} \]
という性質(指数法則)が成り立っています。
2分の1乗とは
さて、\(n,m\)が自然数のときに成り立つ指数法則\((2^{n})^m =2^{n\times m}\)からは、そのままでは分数乗が生まれそうにありません。
逆に、\((2^{n})^m =2^{n\times m}\)が\(n,m\)が自然数でないときも成り立つように、べき乗という概念を拡張するとどうなるでしょうか? 例えば、\(n=\frac{1}{2},m=2\)のときを形式的に書き下してみると
\[ \begin{aligned}(2^{\frac{1}{2}})^2 = 2^{\frac{1}{2} \times 2}=2\end{aligned} \]
が成り立ちます。左辺は\(2\)乗して2になる数なので、2の2分の1乗を
\[ \begin{aligned}2^{\frac{1}{2}}:= \sqrt{2}\end{aligned} \]
と正の平方根で定義しましょう。そうすれば、
\[ \begin{aligned}(2^{\frac{1}{2}})^2 = (\sqrt{2})^2 = 2\end{aligned} \]
という指数法則が、確かに成り立つようになっています。
そもそもルート\(\sqrt{2}\)とはどういう数か、近似値を求める簡単な方法については次の記事を参照してください。
分数乗とは
さらに、\(2^{\frac{1}{3}}\)を\(2\)の3乗根\(\sqrt[3]{2}\)(3乗すると2になる正の数)によって
\[ \begin{aligned}2^{\frac{1}{3}}:=\sqrt[3]{2}\end{aligned} \]
と定義します。すると、ここでも指数法則は
\[ \begin{aligned}(2^{\frac{1}{3}})^3 = (\sqrt[3]{2})^3=2\end{aligned} \]
と成り立ちますね。さらに指数法則に合わせれば、
\[ \begin{aligned}2^{\frac{2}{3}}:=(\sqrt[3]{2})^2\end{aligned} \]
と分数乗を定義することができます。
より一般には、数の分数乗を
\[ \begin{aligned}2^ {\frac{k}{\ell}} := (\sqrt[\ell] {2})^k\end{aligned} \]
\[ \begin{aligned}a^ {\frac{k}{\ell}} := (\sqrt[\ell] {a})^k\end{aligned} \]
と定義しましょう。なぜそう定義するかといえば、指数法則
\[ \begin{aligned}(2^{n})^m =a^{n\times m}\end{aligned} \]
が\(n,m\)が分数(有理数)の場合でも成り立つようにしたかったから、というわけでした。
具体的なイメージを得るために、\(2^{\frac{2}{3}}\)の近似値をラフに求めてみましょう。
\(1\)より大きい数のべき乗は、指数が大きいほど大きな数になるという性質があります。したがって、
\[ \begin{aligned}1= 2^{0} < 2^{\frac{1}{3}}<2^{\frac{1}{2}} \\<2^{\frac{2}{3}} <2^1 =2\end{aligned} \]
となります。\(2^{\frac{1}{2}}\)が約\(1.4\)と知っていれば、\(2^{\frac{1}{3}},2^{\frac{2}{3}} \)といった数が、数直線でどういう位置関係にあるかイメージできるでしょうか。
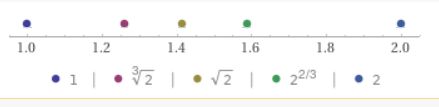
画像引用:WolframAlpha
より精度良く求める方法:ニュートン法によってルート、円周率の近似値を求めてみよう
べき乗とべき乗根の逆関係
ここからは、べき乗によって定まる関数の性質、逆の関係を少し紹介します。
2次関数\(f_2 (x)=x^2\)と2乗根による関数\(f_{\frac{1}{2}} (x) =x^{\frac{1}{2}} \)は、1次関数\(f_1(x) = x\)について対称な形をしています。

関数の合成の言葉を使えば、\(f_2 (f_{\frac{1}{2}}(x))= (x^\frac{1}{2})^2=x\)が成り立ちます。
一般に、\(f(g(x))=x\)が常に成り立つような関数\(f,g\)を、互いに逆関数であると呼びます。\(x^2\)の逆関数は\(x^{\frac{1}{2}}\)です。
\(x^3\)と\(x^{\frac{1}{3}}\)も、互いに逆関数です。
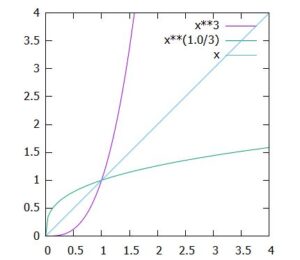
\(x^{\frac{2}{3}}\)の逆関数は、\(x^{\frac{3}{2}}\)です。
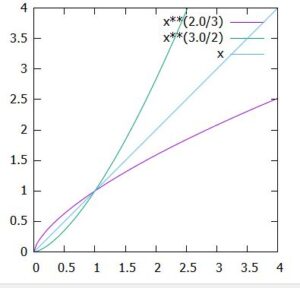
一般に、\(f(x)=x^{\frac{k}{\ell}}\)の逆関数は、\(g(x)= x^{\frac{\ell}{k}}\)です。指数がちょうど逆数になっていますね。実際、指数法則を使って計算すれば、
\[ \begin{aligned}f(g(x))= (x^{\frac{\ell}{k}})^{\frac{k}{\ell}} \\ =x^{\frac{\ell}{k} \cdot \frac{k}{\ell}}= x\end{aligned} \]
が成り立っていますね。
2次関数や3次関数のグラフがイメージできるならば、それを\(f(x)=x\)について折り返したグラフとして\(\sqrt{x},\sqrt[3]{x}\)といった分数次の関数についてイメージできるでしょう。
以上、2分の1乗、分数乗とは何か、指数法則に注目して紹介してきました。分数乗とは
\[ \begin{aligned}2^ {\frac{k}{\ell}} := (\sqrt[\ell] {2})^k\end{aligned} \]
なのだと覚えれば、計算することはできるでしょう。しかしどうしてそう定義するかと言えば、
\[ \begin{aligned}(2^{n})^m =2^{n\times m}\end{aligned} \]
といった指数法則がいつでも(\(n,m\)が分数であっても)成り立っていてほしいからなのです。
分数乗やマイナス乗は、「べき乗=何回か掛ける」という素朴な定義から出発して得られる、指数法則という基本的な性質に合わせて考えられています。\((2^{n})^m =2^{n\times m}\)や\(\frac{2^n}{2^m} =2^{n- m}\)といった指数法則をスムーズに思い出せるようになれば、分数乗やマイナス乗の扱いに困ることはないでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
