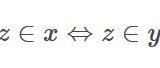線形代数学の応用：CG・画像処理（拡大縮小・反転、回転、せん断）について

どうも、木村（@kimu3_slime）です。

今回は、CG・画像処理には、行列による変換、線形代数学が応用されている話をしたいと思います。Pythonによるプログラム例つきなので、感覚的に理解しやすいと思います。

画像＝点の集まり
画像の変換＝点の変換
こちらもおすすめ

画像＝点の集まり

今回題材にするのは、次の画像です。

この画像は、コンピュータ上でどういう情報として保存されているのでしょうか？　これはピクセルと呼ばれる細かい粒から構成されています。拡大された画像を見てみましょう。

このように、平面が縦横の細かいメッシュによって区切られています。ピクセルのひとつひとつには、色情報が割り当てられています。例えば、青・緑・赤＝\((200, 245, 95)\)といったように、3つの数字の組、すなわち3次元ベクトルとして表されます。\((255, 0, 0)\)なら真っ青、\((0, 0, 0)\)は黒、\((255, 255, 255)\)は白ですね。

参考：色空間 – Wikipedia

題材にした画像のサイズは、\(324 \times 324\)です。つまり、この画像の情報は、\(324 \times 324\)の行列であって、その各成分が1つの色情報からなっているようなもの。細かい網目のひとつひとつに、色が指定されているのです。

（行列の各成分が数ではなくベクトルとなっているとき、それは一般にはテンソルと呼ばれます。ただし、今回は色の変換は考えず、その空間的な配置のみ考えるので、行列として扱えば十分です。）

画像の変換＝点の変換

コンピュータを使えば、様々な形で画像を加工することができます。特に画像の形を変えること、変換には、線形代数学の考え方が役立っているのです。

拡大縮小、反転

まずは、画像の拡大縮小をしてみましょう。

変換前の座標を\((z,w)\)、変換後の座標を\((x,y)\)と書きます。画像を\(x\)軸方向に半分、\(y\)軸方向に2倍にするような変換は

\[ \begin{aligned}\begin{pmatrix} x\\ y \end{pmatrix}= \begin{pmatrix} 0.5 & 0 \\ 0 & 2 \end{pmatrix} \begin{pmatrix} z \\ w \end{pmatrix}\end{aligned} \]

と表されます。例えば\(z=200\)のところにあった色は、\(x=100\)のところに移るわけです。

変換について、こちらでも紹介しました：行列の積の定義はなぜあの形？変換の合成として見る

コンピュータ上で画像を「行列」として取り込み、その行列に行列\(\begin{pmatrix} 0.5 & 0 \\ 0 & 2 \end{pmatrix} \)を施し、そしてそれを画像として戻せば、上の画像が得られるわけです。

プログラミング言語Python、画像の取り込み用ライブラリとしてOpenCVを使ったプログラム例を紹介します。数学におけるベクトルや行列は、numpyのndarrayと呼ばれる配列に対応しています。

import cv2
import numpy as np
import itertools

#画像の取り込み
img = cv2.imread('./data/pict/image1.jpg')
height, width, color = img.shape
print(height)

#拡大縮小
def scaling(A):
    B = np.zeros((2*height,2*width,3),dtype=np.uint8)
    S = np.linalg.inv(np.matrix([[-1,0], [0, 1]]))
    for x,y in itertools.product(range(2*height), range(2*width)):
        z = np.dot(S,[x,y])[0,0] +width
        w = np.dot(S,[x,y])[0,1]
        if z >=0 and z<width and w>=0 and w<height:
            B[y,x] = A[int(w),int(z)]
        else:
            B[y,x] = 0
    return B

#回転
def rotation(A):
    B = np.zeros((2*height,2*width,3),dtype=np.uint8)
    theta = -np.pi / 4
    R = np.linalg.inv(np.matrix([[np.cos(theta),-np.sin(theta)],
     [np.sin(theta), np.cos(theta)]]))
    for x,y in itertools.product(range(2*height), range(2*width)):
        z = np.dot(R,[x,y])[0,0]+250
        w = np.dot(R,[x,y])[0,1]-250
        if z >=0 and z<height and w>=0 and w<width:
            B[y,x] = A[int(w),int(z)]
        else:
            B[y,x] = 0
    return B

#せん断
def shearing(A):
    B = np.zeros((2*height,2*width,3),dtype=np.uint8)
    H = np.linalg.inv(np.matrix([[1,0], [2, 1]]))
    for x,y in itertools.product(range(2*height), range(2*width)):
        z = np.dot(H,[x,y])[0,0]
        w = np.dot(H,[x,y])[0,1]
        if z >=0 and z<height and w>=0 and w<width:
            B[y,x] = A[int(w),int(z)]
        else:
            B[y,x] = 0
    return B

#画像の出力
cv2.imshow("image",shearing(img))
cv2.waitKey(0)
cv2.destroyAllWindows()

import cv2

import numpy as np

import itertools

#画像の取り込み

img = cv2.imread('./data/pict/image1.jpg')

height, width, color = img.shape

print(height)

#拡大縮小

def scaling(A):

B = np.zeros((2*height,2*width,3),dtype=np.uint8)

S = np.linalg.inv(np.matrix([[-1,0], [0, 1]]))

for x,y in itertools.product(range(2*height), range(2*width)):

z = np.dot(S,[x,y])[0,0] +width

w = np.dot(S,[x,y])[0,1]

if z >=0 and z<width and w>=0 and w<height:

B[y,x] = A[int(w),int(z)]

else:

B[y,x] = 0

return B

#回転

def rotation(A):

B = np.zeros((2*height,2*width,3),dtype=np.uint8)

theta = -np.pi / 4

R = np.linalg.inv(np.matrix([[np.cos(theta),-np.sin(theta)],

[np.sin(theta), np.cos(theta)]]))

for x,y in itertools.product(range(2*height), range(2*width)):

z = np.dot(R,[x,y])[0,0]+250

w = np.dot(R,[x,y])[0,1]-250

if z >=0 and z<height and w>=0 and w<width:

B[y,x] = A[int(w),int(z)]

else:

B[y,x] = 0

return B

#せん断

def shearing(A):

B = np.zeros((2*height,2*width,3),dtype=np.uint8)

H = np.linalg.inv(np.matrix([[1,0], [2, 1]]))

for x,y in itertools.product(range(2*height), range(2*width)):

z = np.dot(H,[x,y])[0,0]

w = np.dot(H,[x,y])[0,1]

if z >=0 and z<height and w>=0 and w<width:

B[y,x] = A[int(w),int(z)]

else:

B[y,x] = 0

return B

#画像の出力

cv2.imshow("image",shearing(img))

cv2.waitKey(0)

cv2.destroyAllWindows()

画像の情報が集まった行列は\(A\)、変換結果は\(B\)としています（np.matrix）。また、元の座標\((z,w)\)の情報を使って計算するので、途中で逆行列を求めています（np.linalg.inv）。

拡大縮小の特殊なケースに、反転変換があります。

\[ \begin{aligned}\begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix}\end{aligned} \]

という変換ならば、\(y\)軸に関する反転変換ですし、

\[ \begin{aligned}\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}\end{aligned} \]

ならば、\(x\)軸に関する反転変換です。

変換によっては、画像が描写される範囲の外側へはみ出て表示されなくなります。これは、変換の原点\((0,0)\)が画像の一番左上に設定されているからです。つまり、\((x,y)\)が負になるような領域は設定されていません。

なので、例えば\(x,y\)軸で単純に反転すれば、結果は真っ黒としてしか表示されません。そこで、プログラム内で次のように並行移動してやる必要があるでしょう。ベクトル\(c\)の分だけ動きます。

\[ \begin{aligned}\begin{pmatrix} z\\ w \end{pmatrix}= S \begin{pmatrix} x \\ y \end{pmatrix} + c\end{aligned} \]

回転

画像の向きを調整したい、そんなときは回転変換です。

\[ \begin{aligned}\begin{pmatrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{pmatrix}\end{aligned} \]

で、\(\theta = -\frac{\pi}{4}\)のときは、次のような画像になります。

通常の数学の慣習とは異なり、\(y\)は下側が正の向きとなっていることにも注意しましょう（\(x\)軸は同じ）。したがって、回転変換で通常想定される回転の向きとは、一見逆になっています。

せん断

せん断は、図形をひし形に歪めるような変換です。ずらし変換とも。一方の軸を斜めにする変換とも言えるでしょう。

\(x\)軸に平行なせん断、水平せん断と

\[ \begin{aligned}\begin{pmatrix}1 & 1 \\ 0 & 1\end{pmatrix}\end{aligned} \]

\(y\)軸に平行なせん断、鉛直せん断があります。せん断の傾きは自由に変えられます。

\[ \begin{aligned}\begin{pmatrix}1 & 0 \\ 2 & 1\end{pmatrix}\end{aligned} \]

実は、行列によって表されるあらゆる（正則な線形）変換は、これまでに述べてきた3種の変換、拡大縮小、回転、せん断の組み合わせとして表されることが知られています。基本的な変換を組み合わせることで、多様な変換を生み出せるわけですね。

今回は、コンピュータによる画像の形の加工において、線形代数学、行列による変換の考え方が役立つことを紹介しました。

画像処理にはもっと複雑で面白いものがたくさんありますが、今回の初歩的な例を通して、線形代数が画像処理に役立っていることを感じてもらえたら嬉しいです。

木村すらいむ（@kimu3_slime）でした。ではでは。

世界標準MIT教科書ストラング:線形代数イントロダクション

posted with amazlet at 20.01.16

ギルバートストラング
近代科学社
売り上げランキング: 36,138

Amazon.co.jpで詳細を見る

こちらもおすすめ

行列の積の定義はなぜあの形？変換の合成として見る

なぜ行列式を学ぶ？面積・体積との一致、ヤコビアンへの応用

線形常微分方程式を行列で解く：行列の指数関数を解説