高校数学と大学数学のつながり、違い・ギャップを解説

どうも、木村（@kimu3_slime）です。

今回は、大学の数学科で数学を学んだ僕が、高校数学と大学数学の違い・ギャップ、つながりを解説しようと思います。

高校数学と大学数学のつながり
高校数学と大学数学の違い・ギャップ
こちらもおすすめ

高校数学と大学数学のつながり

そもそも、「高校数学」「大学数学」とは

「高校数学」「大学数学」とおおざっぱに言っているわけですが、最初にその意味を確認しておきましょう。

高校数学には、数学I、II、III、A、B、Cなど、まず国（学習指導要領）によって定められた内容たち、教科書高校数学があります。

そしてあえて高校数学というとき、それは受験数学、または試験数学を指していることもあります。受験数学においても、マーク式の数学と、記述式の数学では、内容が違ってきますね。

参考：大学数学のロードマップ～分野一覧と学ぶ順序

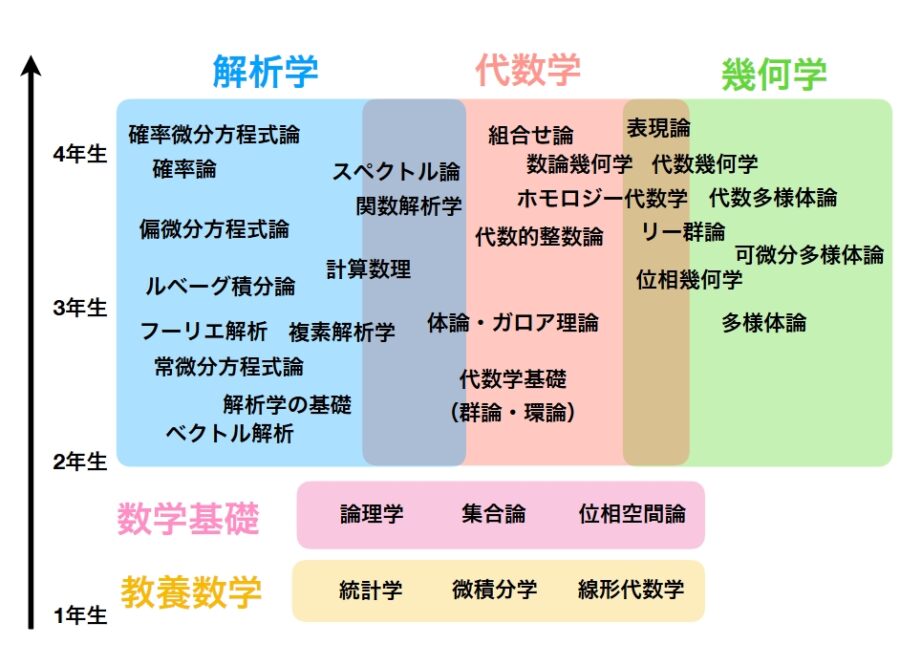
大学数学が意味するところは、おおざっぱに2種類あるかと思います。科学、もとい理工系学部で基礎となる、統計学、微積分学、線形代数学などの教養数学。そして、数学科のみが扱う専門数学、または純粋数学です。

教科書高校数学は教養数学につながる

よく高校数学と大学数学は別物である、そのことが強調して言われたりしますが、僕は全くそうは思いません。

大学数学、特に教養数学は教科書高校数学の延長です。

場合の数と確率・データの分析→統計学
三角関数・指数関数・数列・極限・微分・積分→微積分学
図形と方程式・ベクトル・平面上の曲線・複素数平面（・行列）→線形代数学

高校数学を身に着けていることは、教養数学の取得に非常に役立ちます。数学は積み重ねの学問であり、もちろん高校数学もベースのひとつです。また、教養数学は高校数学の一種のリメイクのような部分があります。

計算能力は共通して使える

受験数学もまた、大学数学の役に立ちます。受験数学＝パズル・技巧的だから、「本物の数学」の役に立たないと考えるのは、愚かなことです。

僕が大学に入ってから、受験数学が役立ったと感じたのは、そこで培った計算能力が筋肉のようなものになっていたことです。大学の数学だけでなく、物理学や化学を学ぶときにも、高校レベルの計算がスムーズに行えるようになっていることは大事です。それが呼吸レベルに当たり前のものになっているからこそ、より先の議論が、何をしたいか把握する余裕を持てるようになります。

大学数学が高校数学では見られないほどに論理を重視し、抽象性を帯びるからといって、式に従って記号を操作する能力や、パターンマッチして議論を進める能力は、役に立たなくなるわけではありません。

また、受験数学の記述式試験において、難しい問題に向かい合う力は、大学数学の問題に向かい合う力と何も変わりません。同じ問題に長時間向かいあって考え続ける能力は、学問、もとい数学の基礎体力です。

高校数学と大学数学の違い・ギャップ

では、高校数学と大学数学の違い、ギャップを述べていきましょう。

論理をベースにするようになる

大学の数学では、高校までに比べて論証が重視されます。重視されるというか、論理、特に数理論理学・命題論理が数学の基礎となっているのです。高校までの数学は、素朴な、日常的な感覚に頼った議論が含まれています。

この違いは、教科書のスタイルにも反映されます。大学数学の教科書は、「定義→命題→証明」の繰り返しが基本です。「当たり前」に思えそうな事実も、証明しなければ正しいとは考えません。僕は最初に論理を身につけることの重要さに気づかず、大学数学につまづきました（笑）。

参考：大学数学の教科書の読み方、最初に「定義・命題・証明」を知ろう

論理を重視する違いを表す有名な例としては、数列\({a_n}\)の極限・収束の定義があります。

高校数学
\(n\)が限りなく大きくなっていくとき、\(a_n\)がある一定の値\(\alpha\)に限りなく近づいていくとき、数列\({a_n}\)は\(\alpha\)に収束するという。
大学数学
数列\({a_n}\)は\(\alpha\)に収束するとは、次の条件を満たすこと。任意の\(\varepsilon>0\)に対し、番号\(N\)で、\(n\geq N\)ならば\(| a_n – \alpha|<\varepsilon\) を満たすようなものが存在する。
\((\forall \varepsilon >0)(\exists N\in \mathbb{N} ) (\forall n \in \mathbb{N})(n \geq N \Rightarrow |a_n – \alpha|<\varepsilon)\)

大学数学は、「限りなく近づく」ことの意味をより明確にしたもので、これはイプシロン-エヌ論法（イプシロン-デルタ論法）と呼ばれる定義です。

この議論でつまづいて、大学数学が苦手になったり、あるいは自分に手の届かないものだと思ってしまう人がいるようです。これを理解するためには、例えば存在命題・全称命題や、論理記号の扱いを知っておいた方が良いでしょう。

参考：集合論のはじまり、全称命題と存在命題、論理記号を知ろう

より抽象的になる

大学に入ると、生物は化学に、化学は物理に、物理は数学に、数学は哲学になる

というような話を、大学生の頃に聞きました。小話としては面白いのですが、正しいかというと僕はそうではないなと、数学科に進んでから思うようになりました。（そもそも、大学1年次は、高校では分断されていた科学の科目を、垣根を取り払い、相互に参照した上で整理し直す時間になるでしょう）

とはいえ、数学がより抽象的になる、というのは正しいと思います。

これを最初に感じるのは、線形代数学ではないでしょうか。行列やベクトルについて、高校では2-3次元のものしか扱いませんが、大学ではそれより多い、一般の\(n\)次元を扱います。

抽象的になると、直感が通用しなくなり、ついていけない人が出てきます。僕も少しそういう面がありました。

抽象的な学問の勉強には、コツがあります。とにかく自分で簡単な具体例を作るということです。いきなり\(n\)を考えるからわからなくなるのであって、「\(n=1\)のとき、\(n=2\)のときはどうか？」と具体的に進めれば、高校数学や既存の知識から、順序立てて進むことができます。

抽象化が進むと、感覚が頼りにならなくなる分、正しい論証を行う自信が求められます。書いてあることを眺めるだけでなく、ノートを取りながら、自分に何がわかっていて何がわかっていないか、それを把握していれば、抽象化も怖くありません。「わからない」と気付けるのは、悪いことではなく良いことです。

参考：「自明、明らかである」に気をつけて、疑いながら数学書を読もう、数学の学びを深めるために必要なのは、「わからない」と言える力

また、抽象化された学問がポンと与えられると、「それは何の役に立つの？」と思いたくなります。その学問を学ぶ意義、その応用を、大学数学の教科書や授業は、あまり与えてくれないことがあります。

実際に、自分の専門分野の勉強を初めてみて、そこで教養数学が使われているのを知ってから、基礎を固める、という勉強方法も良いでしょう。

線形代数ならば、Googleの検索順位付けに、\(n\)次元の行列・固有値問題が必要になってくることを紹介しました。

参考：なぜ線形代数を学ぶ？ Googleのページランクに使われている固有値・固有ベクトルの考え方

学ぶペースが速くなるが、サポートは少なくなる

大学の講義は、高校の授業に比べ、単純に時間数が増えます。つまり、それだけ多くの内容を短期間に学ぶようなカリキュラムになっているのです。

僕のようにボケっとしていると、いつの間にか次の講義の内容についていけなくなり、置いていかれます。「誰もがついてきているか？」といったことは、気にせずに講義は進められます。ついてこれないならば、単位が取れないだけです。

高校までは何も考えずとも進級できるようなシステムになっていることが多いですが、大学では学ぶための自主性が求められます。自分一人で内容についていけないならば、図書館で本を探したり、友達やTAや先生に教えを乞う必要があります。数学科の専門数学になれば、友人と教科書を選び、ゼミ・勉強会を行うのも良いでしょう。

教科書・参考書も、高校までに比べると種類が少なくなり、不親切に感じられることもあるでしょう。演習問題に、答えが書かれているとは限らなくなります。

その分、教科書やカリキュラムは高校までに比べて柔軟になります。学びたいことを学ぶのに、順序はありません。必要だと思うことを、良さそうな本を選んで学んで行く必要があるでしょう。

当サイト「趣味の大学数学」では、独学におすすめの教科書・参考書を紹介しています。

高校数学と大学数学のつながり、違い・ギャップを解説を解説してきました。

確かに、僕は大学数学を学び始めるときにつまづいて、ギャップを感じました。一方で、「数学の学び方」を誰かが教えてくれたら、もう少しそのギャップは減らせたなと思います。

大学数学には、高校数学までと本質的な難しさの違いはないと思っています。大学数学はとても面白いし、それは数学科や天才だけのものにしてしまうには、もったいないです。

「趣味の大学数学」は、高校数学を学んだ人が、スムーズに大学数学に入門できるような情報を増やしていきます。大学数学に気軽に楽しく触れてる人が増えれば嬉しいです。

木村すらいむ（@kimu3_slime）でした。ではでは。