どうも、木村(@kimu3_slime)です。
熱や物質が空間を伝わっていく現象を、伝播(でんぱ propagation)と言います。
生き物がある空間に繁殖して広がっていったり、特定の遺伝子が増えたり、燃焼によって熱が広がったり、伝染病が広がったり……。
参考:伝染病伝播の反応拡散モデルについて(<特集>感染症の数理モデル) – 細野 雄三
そんな伝播現象をとらえるモデルとして、フィッシャー方程式を簡単に紹介します。
フィッシャー方程式
\(u(x,t)\)を個体数や熱量を表す関数として、フィッシャー方程式は、次のような偏微分方程式です。
\[ \begin{aligned}\frac{\partial u}{\partial t}= \Delta u + u(1 – u) \quad x\in \mathbb{R}^N, t>0\end{aligned} \]
偏微分方程式の基礎知識:なぜ偏微分を学ぶ? フーリエの熱伝導方程式を例に、花粉の広がりを数式で予測する、拡散方程式とは
この方程式は、以前に紹介したロジスティック方程式の拡張となっています。
\[ \begin{aligned}\frac{du}{dt}= u(1 – u)\end{aligned} \]
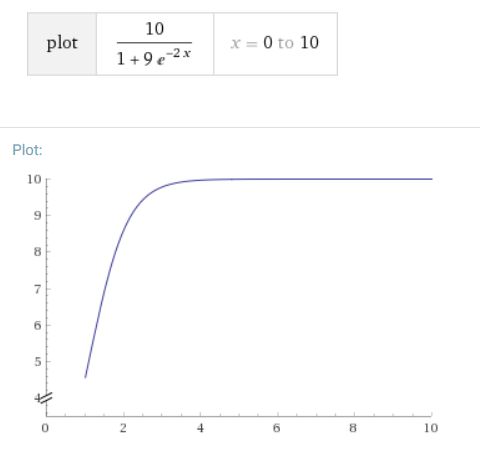
ロジスティック方程式では、正の初期値から出る解は\(t\to \infty \)で\(1\)に近づいていきます。生物の個体群として見るなら、一定の密度まで増えて増加が落ち着く過程としてとらえられます。
フィッシャー方程式は、統計学者のロナルド・フィッシャー(Fisher)が、対立遺伝子が生物集団の間に世代交代によって広がっていく現象を説明しようとして考え出されました(集団遺伝学)。コルモゴロフ、ペトロフスキー、ピスクノフによっても扱われた方程式であるため、フィッシャー-KPP方程式とも呼ばれます。
(経済学者アービング・フィッシャーのフィッシャー方程式とは別物です。)
参考:Fisher, The Genetical Theory Of Natural Selection, (1937). A. Kolmogorov, I. Petrovskii, and N. Piscunov, A study of the equation of diffusion with increase in the quantity of matter, and its application to a biological problem,(1937)
フィッシャー方程式の解は、どのように振る舞うのでしょうか?
ロジスティック方程式では考えていない空間的な分布で、拡散\(\Delta u\)を考えていますが、挙動は似たものになります。
初期値\(u_0\)が\(u_0 \not \equiv 0 \)で、ある定数\(M\geq 1\)により \(0 \leq u_0(x) \leq M\) を満たすとする。
このとき、フィッシャー方程式の解は時間大域的に存在して、\(\mathbb{R}^N\)の任意の有界集合上で一様に\(u(x,t)\to 1\quad (t\to \infty)\) を満たす。
参考:柳田「反応拡散方程式」 p.88

画像引用:柳田「反応拡散方程式」
\(u=0\)はすべて死滅した状態です。しかしここで、少しでも正の部分があるなら、(最初は他の場所が0であっても)空間のすべての場所で\(u=1\)に近づいていきます。
生物の個体数の変動として見れば、わずかな個体が空間に侵入しただけで、大繁殖を起こす現象です。伝染病の増殖と考えれば、なんとも厄介です(笑)。このような現象は、刺激に敏感に反応するという意味でヘアトリガー効果(hair-trigger effect)と呼ばれています。
解は\(1\)に近づくとして、どのように近づくのでしょうか?
上の図で見るように、0でない場所では素早く1に近づき、増えた場所から拡散によって空間(横方向)に広がっていく、進んでいく波が観察される……。そんな予測が、数学的に正しいことが知られています。
波の形を保ったまま伝播する解を、進行波解(progressive wave solution)と呼びます。
\(N=1\)とする。
\(c\geq 2\)に対し、フィッシャー方程式には進行波解\(u = \varphi(z),z= x- ct\)が存在する。それは位相のずれを除いて一意。
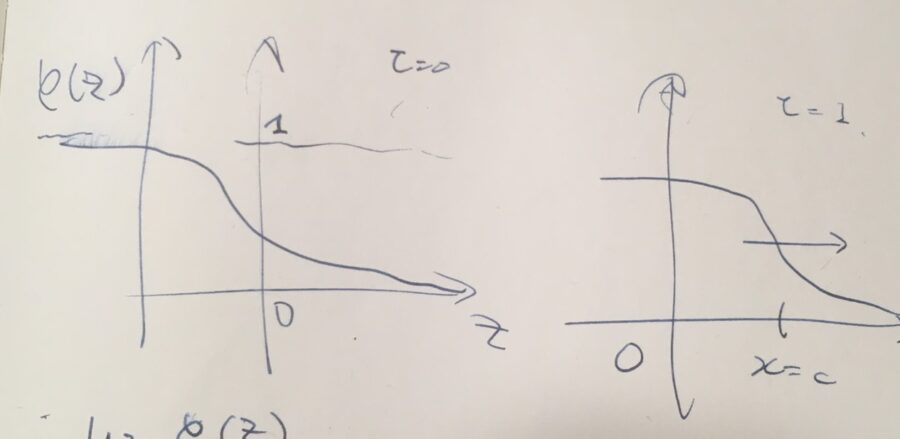
そして、\(\varphi(z)\)は\(z\)につき単調減少で、\(\varphi (z) \to 1 \quad (z\to -\infty)\)、\(\varphi (z) \to 0 \quad (z\to \infty)\)を満たす。(このような解を、フロント型進行波解という)
参考:柳田「反応拡散方程式」 p.91
進行波解は、\(t=0\)のとき、\(u_0 =\varphi (x)\)ですが、\(t=1\)で\(u(x,1) =\varphi (x -c)\)と\(x\)の正の方向へ進んでいき、時間とともに形を保ったまま進みます。これがまさに伝播を表す解です。
このような進行波解は、ある意味で安定であることが知られていて、フィッシャー方程式の解は進行波解に近づくような挙動をします。
進行波解を持つ方程式
フィッシャー方程式を少し変形した方程式にも、進行波解が存在することが知られています。
南雲方程式(Nagumo equation)
\[ \begin{aligned}\frac{\partial u}{\partial t}= \Delta u + u(u-a)(1 – u) \quad x\in \mathbb{R}^N, t>0,0<a<1\end{aligned} \]
アレン-カーン方程式(Allen-Cahn equation)
\[ \begin{aligned}\frac{\partial u}{\partial t}= \Delta u + u(1- u^2) \quad x\in \mathbb{R}^N, t>0\end{aligned} \]
チェイフィー-インファンテ方程式(Chafee-Infante equation)
\[\frac{\partial u}{\partial t}= \Delta u + \mu ^2 u(1- u^2) \quad x\in [0,L],\mu>0 \\ \frac{\partial u}{\partial x} (0,t) = \frac{\partial u}{\partial x} (L,t) = 0 \]
例えば南雲方程式は、デジタル回路を伝播する波、(双安定な)信号伝送線路の振る舞いのモデルとして提唱されました。
参考: J. Nagumo ; S. Yoshizawa ; S. Arimoto, Bistable Transmission Lines (1965)
空間を伝わって広がっていく波、伝播現象を見かけたら、フィッシャー方程式を思い出してみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
共立出版
売り上げランキング: 45,073
こちらもおすすめ
食う-食われるの数学:捕食者-被食者モデル(ロトカ・ヴォルテラ方程式)とは?




