どうも、木村(@kimu3_slime)です。
普段意識することはありませんが、僕たちの体の中には神経が通っていて、脳からの電気信号によって体を動かしています。
今回は、神経における電気信号の伝播を調べようとして発見された、ホジキン-ハクスリー方程式、およびフィッツヒュー-南雲方程式について紹介します。
ホジキン-ハクスリー方程式
生物学者のホジキンとハクスリーは、ヤリイカの神経線維を調べました。
神経線維は、軸索とも呼ばれる、神経細胞から伸びる突起です。この軸索の上を走る電流(イオンの移動)に注目しています。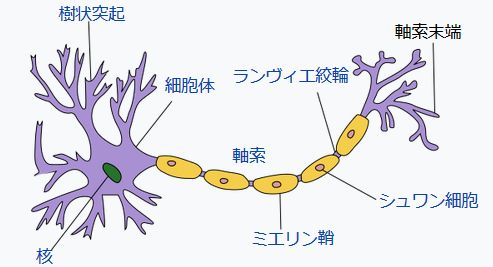
画像引用:File:Neuron-no labels2.png, Quasar Jarosz – Wikipedia
ホジキン-ハクスリー方程式(Hodgkin-Huxley equation)は、次のような4成分の偏微分方程式です。
\frac{\partial u }{\partial t } &= \frac{\partial ^2 u }{\partial x^2 } + f(u,\boldsymbol{v})\\
\frac{\partial \boldsymbol {v}}{\partial t } &= \boldsymbol{g}(u,\boldsymbol{v} ) \\
\
ここで\(u(x,t)\)は神経の電位を表す関数で、\(\boldsymbol{v}(x,t)\)は神経膜の状態を表す3次元ベクトル値関数。\(f,\boldsymbol{g}\)は、神経膜の働きを表す非線形の関数です。
ホジキンとハクスリーの論文では、コンピュータによる数値計算で、次のような形の活動電位の変化を導きました。
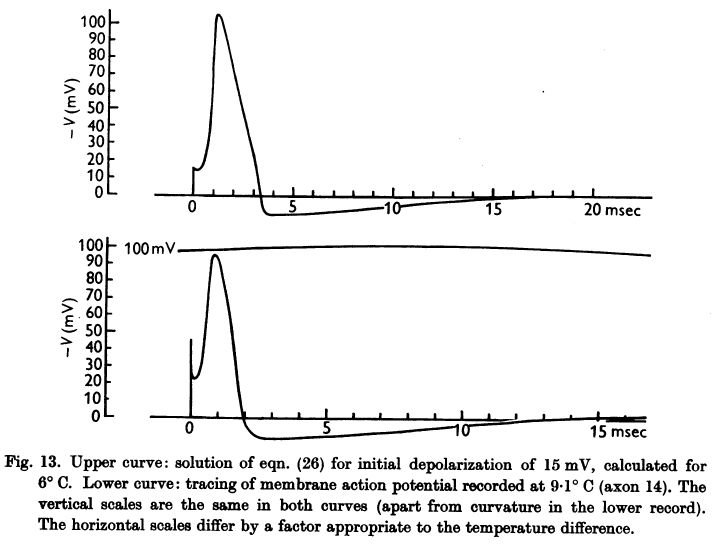
参考:A. L. Hodgkin
A. F. Huxley, A quantitative description of membrane current and its application to conduction and excitation in nerve
彼らは、神経細胞の活動電位の研究により、ノーベル生理学・医学賞を受賞しました。
実験データをよく説明する式ができあがれば、シミュレーションによって神経の研究をより調べることもできるようになることでしょう。
フィッツヒュー-南雲方程式の進行波解
ホジキン-ハクスリー式は、成分数が多く、数学的に調べるのが難しいです。
そこで、その方程式の本質をできるだけ失わないようにして簡略化された方程式、フィッツヒュー-南雲方程式(Fitzhugh-Nagumo equation)が導かれました。
\frac{\partial u }{\partial t } &= \frac{\partial ^2 u }{\partial x^2 } + u(1-u)(u-a) -v \\
\frac{\partial v}{\partial t } &= \varepsilon (u- \gamma v) \\
\
ここで、\(\varepsilon >0,\gamma\geq 0 , 0<a<\frac{1}{2}\)です。
参考:FitzHugh R. (1961) Impulses and physiological states in theoretical models of nerve membrane.、Nagumo J., Arimoto S., and Yoshizawa S. (1962) An active pulse transmission line simulating nerve axon.
神経には、小さな刺激には反応せず、閾値(threshold value)と呼ばれる値より強い刺激を与えると興奮するという特徴があります。
フィッツヒュー-南雲方程式で拡散項を含まない式の相図は、次のようになります。(拡散効果を考えても、同様の結論が導けることが知られています)
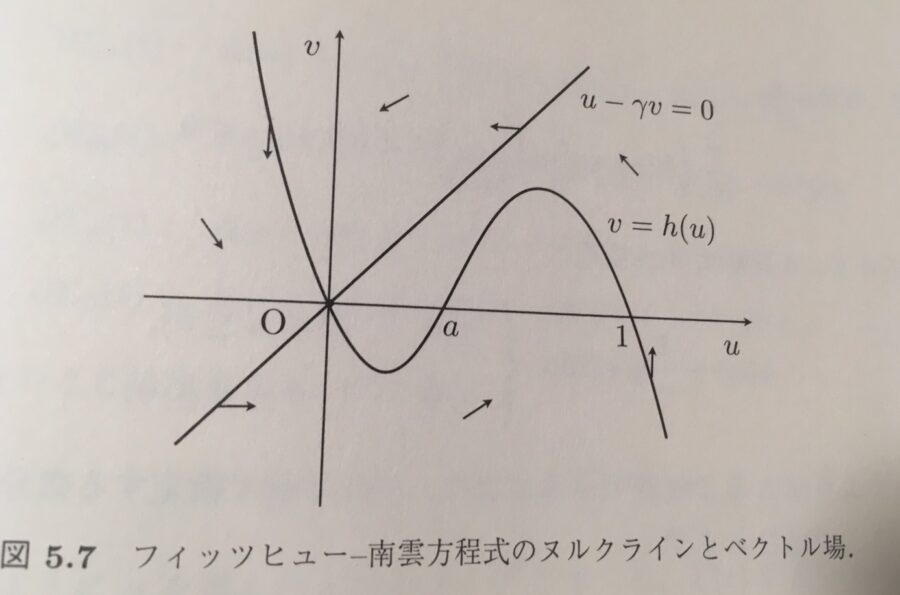
画像引用:柳田「反応拡散方程式」
\((0,0)\)は神経が静止している状態です。\((0,0)\)に近い状態は付近にとどまり続けますが、\((a,0)\)より右側から出発すると大きく\((u,v)\)が増えてから落ち着きます。まさにこれは閾値のモデルとなっているわけですね。
また、神経細胞間をつなぐ軸索を伝播する電気信号の波は、数学的には進行波として捉えられます。
進行波解とは、一定の形を保ちながら一定の速度で特定の空間方向に進む解のことです。
この方程式では、孤立パルス進行波が存在することが知られています。パルス波とは、ホジキン-ハクスリー方程式の図で示されたような、急激な変化をする信号のこと。
そして、ある程度早いパルス波解が安定であり、遅いパルス波解は不安定であることが知られています。
つまり、静止状態\((u,v)=(0,0)\)にちょっとした変化が起こっても静止したままですが、大きな変化を与えればパルス波の方に近づいていく現象が起こっているわけです。
これは全か無かの法則(all-or-none principle)と呼ばれるもの。
静止状態とパルス波が安定で、中途半端な状態が起こらないということは、伝わっている間に多少のズレやノイズが入っても正確に情報が伝わるということ。
改めて、神経というのはよくできているのだと感じられますし、それが数式の上でも再現できるのは面白いですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
こちらもおすすめ
食う-食われるの数学:捕食者-被食者モデル(ロトカ・ヴォルテラ方程式)とは?