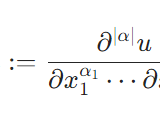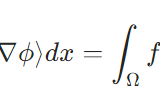どうも、木村(@kimu3_slime)です。
今回は、境界で0のソボレフ空間\(W_0^{k,p},H_0^k\)とは何か紹介します。
導入
\(\Omega \subset \mathbb{R}^N\)を開集合としましょう。ラプラス方程式
\[- \Delta u =f \quad(x\in \Omega)\]
のような偏微分方程式の問題では、\(\Omega\)上の関数\(u\)に対し、ディリクレ境界条件
\[u(x) = 0 \quad (x \in \partial \Omega)\]
を考えることがあります。\( \partial \Omega\)は\(\Omega\)の境界です。
方程式を強微分でなく弱微分として捉えて解を構成しようと思うならば、「ソボレフ空間\(W^{k,p},H^k\)の関数であって、かつ境界で0の値を取る関数」が必要になります。
つまり、素朴には
\[H^1_0 =\{u \in H^1 \mid \partial \Omega 上で u=0 \}\]
\[W_0^{k,p}=\{u \in W^{k,p} \mid すべての|\alpha|\leq k-1 に対し、\\ \partial \Omega 上で D^{\alpha}u=0\}\]
といったように定義したくなります。
しかし、境界上での値を考えるのは、ソボレフ空間、\(L^p\)の関数としては困難です。一般に、測度0の集合を除いて一致する関数\(u =v \, \mathrm{a.e.}\)は、同一視しています。
そして、境界は、全体の測度において測度0の集合になります。1次元の測度(長さ)において端点は測度0、2次元の測度(面積)において曲線は測度0、3次元の測度に(体積)おいては曲面積は測度0、といった具合です。
境界=測度0の集合では、関数の値は定義されているとは限らないのです。
近似による定義
そこで、境界で0の値を取る関数、テスト関数\(C_c^\infty(\Omega)\)によって近似できる関数として、
\[W_0^{k,p}(\Omega):= \overline{C_c ^\infty(\Omega)}^{W^{k,p}}\]
\[H_0^{k}(\Omega):= \overline{C_c ^\infty(\Omega)}^{H^{k}}\]
と定義しましょう。
上の線は閉包を表しますが、ソボレフ空間\(W^{k,p},H^k\)のノルムに関する閉包を考えていることに注意しましょう。つまり、\(u \in W_0^{k,p}\)とは、
\[\lim_{n\to \infty} \|u_n-u\|_{W_0^{k,p}}=0\]
を満たす\(u_n \in C_c^\infty(\Omega)\)が存在することです。
\(W_0^{k,p}(\Omega)= \overline{C_c ^\infty(\Omega)}^{W^{k,p}}\)という関係性は、\(W_0 ^{k,p}\)において\(W^{k,p}\)のノルムに関して\(C_c ^\infty\)は稠密であると言われます。
また、\(W_0^{k,p}\)は\(W^{k,p}\)のノルムに関する\(C_c ^\infty\)の完備化(completion)であるとも呼ばれます。これは\(W^{k,p}\)が完備で、完備距離空間の閉部分集合は完備であることが理由です。
具体的なイメージは持ちにくいかもしれませんが、少なくともテスト関数そのものは\(W_0^{k,p},H^k\)の要素です。確かに境界で値が0となっていて、弱微分も可能ですね。
境界での値:トレース
ソボレフ空間の関数の境界での値を捉えるために、トレース作用素(trace operator)というものが知られています。
長くなるので詳しくは踏み込みませんが、次のようなものです。
\(\Omega\)は有界な開集合で、境界が\(C^1\)級とする。有界な線形作用素\(T: W^{1,p}(\Omega)\to L^{p}(\partial \Omega)\)で、次の条件を満たすものが存在する。
- すべての\(u\in W^{1,p}(\Omega) \cap C(\overline{\Omega})\)に対し、\(\partial \Omega\)上で\(Tu(x) = u(x)\)
この作用素\(T\)をトレース作用素といい、\(Tu\)を\(u\)のトレースという。
\(u \in C(\overline{\Omega})\)とは境界まで込みで定義された連続関数で、その関数と境界での値が一致するような対応\(Tu\)が考えられます。
\(u \in W^{1,p}(\Omega)\)の境界での値は一般に定義されていませんが、トレース作用素\(T\)を介することで、\(Tu\)という境界での値を考えることができるわけですね。
トレースを用いると、さきほどの関数空間が次のようにも捉えられます。
\[u\in W_0^{1,p}(\Omega) \Leftrightarrow u\in W^{1,p}かつ\partial \Omega上でTu=0 \]
\[u\in H_0^{1}(\Omega) \Leftrightarrow u\in H^{1}かつ\partial \Omega上でTu=0 \]
まさに、弱微分可能かつ境界での値(トレース)が0というわけです。
この条件を用いて、\(H_0 ^1\)の関数の例を考えてみましょう。
\(\Omega =(-1,1)\)、\(u(x) = -|x|+1\)とします。
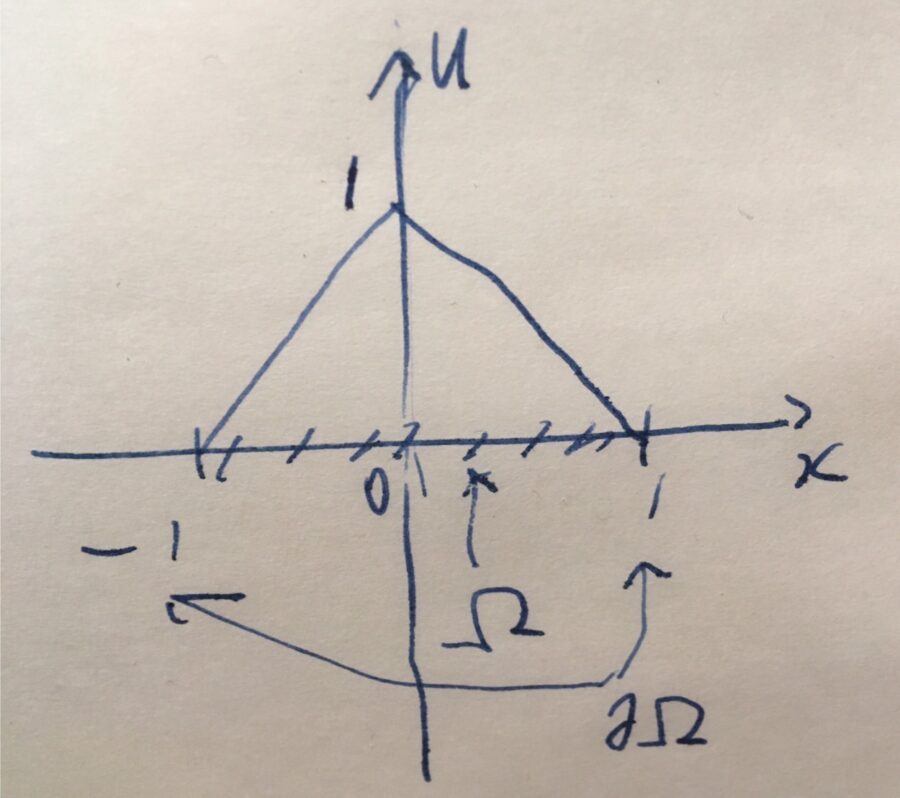
原点において尖っているため、強微分可能ではありませんが、弱微分は可能です。つまり\(u \in H^1\)です。
\(u\)のトレースを\(Tu\)とします。\(u\)は\(\overline{\Omega}= [-1,1]\)で定義された連続関数です。そして\(\partial \Omega =\{-1,1\}\)において、\(u(-1)=u(0)=0\)です。したがって、\(\partial \Omega\)上で\(Tu(x)=u(x)=0\)です。
よって、「 \(u\in H^{1}かつ\partial \Omega上でTu=0\)」、すなわち\(u \in H_0 ^1\)が示せました。
以上、境界で0のソボレフ空間\(W_0^{k,p},H_0^k\)とは何かを紹介してきました。
ラフなイメージとしては、ソボレフ空間に属していて、かつ境界での値が0になることです。ただし、境界での値が0を表現するために、テスト関数による近似やトレースといった議論が必要になるわけでした。
木村すらいむ(@kimu3_slime)でした。ではでは。
Evans, Lawrence C.(著)
¥16,299 (2022-08-19時点)
こちらもおすすめ
ソボレフ空間W^{k,p},H^kとは:多重指数、ノルム、内積