どうも、木村(@kimu3_slime)です。
今回は、三角形の辺の長さと、向かい合う角の大きさの大小関係が一致することの証明を紹介します。
辺が長いならば、角が大きいこと
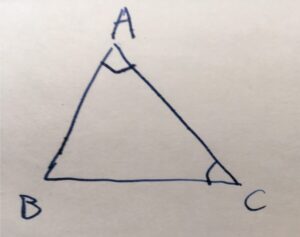
辺の長さが\(AB < BC\)となる三角形\(\triangle ABC\)を考えましょう。
このとき、その辺に向かい合う角の大きさはどちらが大きいでしょうか。長い辺に対応する角の方が、必ず大きくなる気がしますね。
実際、\(\angle BCA < \angle CAB \)となることを証明できます。角を分割して比較していく方針です。
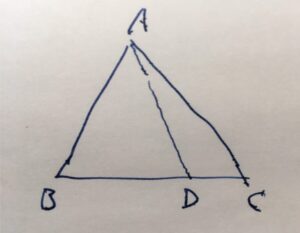
仮定\(AB < BC\)と定規(公準)によって、\(AB = BD\)となる点\(D\)を線分\(BC\)内に描くことができます。
\(AB =BD\)となる二等辺三角形ができ、その底角は等しいので、\(\angle BAD =\angle BDA\)です。
角度の分割(angle-addition postulate)によって、\(\angle CAB = \angle BAD + \angle CAD\)です。\(AD,AC\)は同一の直線上にないので、\(\angle CAD >0\)です(protractor postulate)。したがって、\(\angle BAD < \angle CAB\)となります。
また、\(\triangle CAD\)に注目すると、\(\angle ADB\)はその外角です。したがって、\(\angle ADB = \angle ACD + \angle CAD\)となります。 \(\angle CAD>0\)なので、\(\angle ACD < \angle ADB \)です。
以上をまとめると、\(\angle BAD =\angle BDA\)から\(\angle BCA =\angle ACD < \angle BDA \)で、かつ\(\angle BAD < \angle CAB\)です。よって、不等式の性質(推移律)より、\(\angle BCA < \angle CAB \)が示せました。
角が大きいならば、辺が長いこと

さきほどの逆の事実も成り立ちます。
角度の大きさが\(\angle BCA < \angle CAB \)となる三角形\(\triangle ABC\)を考えましょう。
このとき、対応する反対側の辺の長さについて、\(AB < BC\)が成り立ちます。
証明しましょう。対偶法として、\(AB \geq BC\)と仮定し、\(\angle BCA \geq \angle CAB \)が成り立つことを示します。
\(AB =BC\)のときは、二等辺三角形となるので、確かに底角が等しくなり、\(\angle BCA =\angle CAB \)が成り立ちます。
\(AB >BC\)のときを考えましょう。さきほど示したことから、長い辺に対応する角度は大きい、\(\angle BCA > \angle CAB \)です。
よって、いずれのケースでも\(\angle BCA \geq \angle CAB \)が成り立ちます。対偶が示せたので、\(AB < BC\)が成り立つことが示せました。
以上、三角形の辺の長さと、向かい合う角の大きさの大小関係が一致することの証明を紹介してきました。
この事実は、直線と点を結ぶ最短の線分は垂線であることの証明の基礎となるものです。
図を描けば、確かに長さと角度の大小には対応関係があるのはわかります。こうした当たり前のことでも、幾何学では証明を与えられるのが面白いですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Elementary Geometry for College Students 5th (Fifth) Edition byAlexander
¥13,970 (中古品)