図形の線対称・点対称とは：行列変換の立場から

どうも、木村（@kimu3_slime）です。

今回は、線対称・点対称とは何か、行列変換の観点から紹介します。

線対称と反転変換
点対称と回転変換
こちらもおすすめ

線対称と反転変換

線対称な図形とは、ある線を軸として図形を反転させても重なり合う図形のことです。

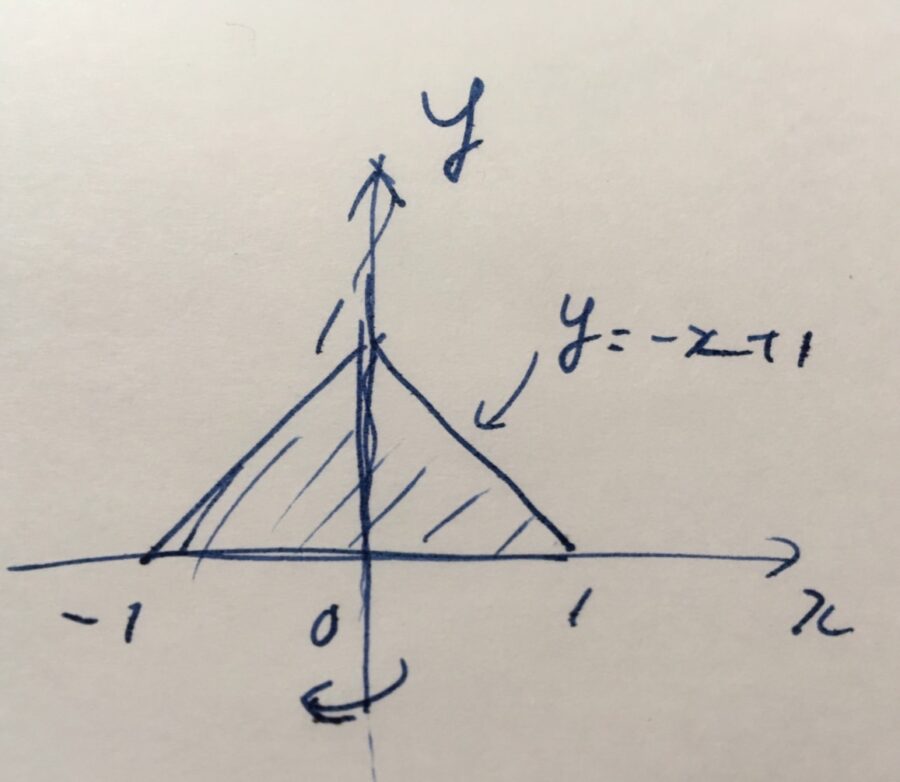
例えば、上の図の三角形は、\(y\)軸（\(x=0\)）という直線を軸として線対称です。日常的には、左右対称といったりしますね。

これを行列の言葉で表現してみましょう。線対称な図形とは、反転変換によって変わらない（不変な）図形のことです。

\(y\)軸を軸とした反転変換は、

\[ A_Y = \begin{pmatrix} -1 &0 \\0 &1 \end{pmatrix}\]

と表せます。

三角形の辺の右上側、\(y= -x+1\)をこの行列で変換してみましょう。

\[ \begin{aligned} & \begin{pmatrix} -1 &0 \\0 &1 \end{pmatrix} \begin{pmatrix} x\\-x+1 \end{pmatrix}\\ &= \begin{pmatrix} -x \\-x+1 \end{pmatrix} \end{aligned}\]

となるので、\(X= -x\)とおけば、\(Y = -x+1 = X+1\)という直線に写っています。\(x\)が0から1へと動くとき、\(X\)は0から-1へと動き、それに伴い\(Y\)は1から0へと動きますね。これは左上側の辺です。

\(x\)軸上の点\((x,0)\)を反転させれば

\[ \begin{aligned} & \begin{pmatrix} -1 &0 \\0 &1 \end{pmatrix} \begin{pmatrix} x\\0 \end{pmatrix}\\ &= \begin{pmatrix} -x \\0 \end{pmatrix} \end{aligned}\]

へと写ります。\(x\)が\(0 \leq x \leq 1\)を動くとき、\(-x\)は\(-1 \leq x \leq 0\)の範囲を動きますね。これで下側の辺が線対称であることが確かめられました。

\(x^2 ,\sin x\)のように、\(f(x)=f(-x)\)を満たす関数\(f\)は、偶関数と呼ばれます。偶関数のグラフは、\(y\)軸について線対称です。

グラフ上の点\((x,f(x))\)を反転変換すると、\((-x, f(x)) = (-x,f(-x))\)となるので、\(x\)の正の部分のグラフと、負の部分のグラフが対応しているわけです。

\(x\)軸を軸とする反転変換は、

\[ A_X = \begin{pmatrix} -1 &0 \\0 &1 \end{pmatrix}\]

と表せます。一般的な直線を軸とする反転変換は、これらに回転行列と平行移動を組み合わせれば良いですね。

ある関数とその逆関数は、直線\(y=x\)について線対称であることが知られています。

点対称と回転変換

点対称な図形とは、ある点を中心として図形を反転させても重なり合う図形のことです。2次元では、それは180度回転させて重なり合う図形のことです。

これは180度の回転行列

\[ R_{\pi} = \begin{pmatrix} -1 &0\\0&-1 \end{pmatrix}\]

によって不変な図形と言い換えられます。

\(X\)という文字を模した図形、\(y=2x\)と\(y=-2x\)のグラフを重ねた図形について考えましょう。

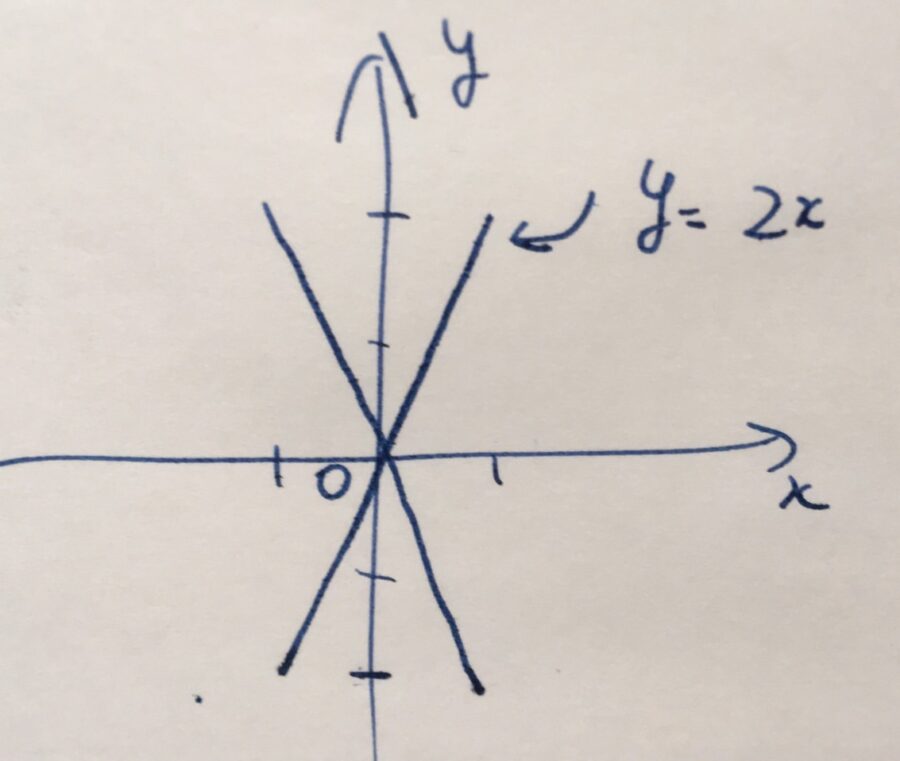
\(y=2x\)上の点を回転変換させると、

\[ \begin{aligned} & \begin{pmatrix} -1 &0 \\0 &-1 \end{pmatrix} \begin{pmatrix} x\\2x \end{pmatrix}\\ &= \begin{pmatrix} -x \\-2x \end{pmatrix} \end{aligned}\]

なので、同じく\(y=2x\)上の点となります。

\(y=-2x\)上の点も、\((-x, 2x)\)へと写るので、\(y=-2x\)上の点です。

よって、この図形は点対称であることが示せました。

\(x^3 ,\cos x\)のように、\(f(x)=-f(-x)\)を満たす関数\(f\)は、奇関数と呼ばれます。奇関数のグラフは、原点について点対称です。

グラフ上の点\((x,f(x))\)を回転変換すると、\((-x, -f(x)) = (-x,-f(-x))\)となるので、変換後の点も元のグラフ上の点であることがわかります。

回転変換は、一般に180度でなくても考えることができます。2次元においては、点対称な図形とは、回転不変な図形の特殊なケースと言う事ができますね。

以上、線対称・点対称とは何か、行列変換の観点から紹介してきました。

線対称や点対称という考え方を合わせた対称性の分析は、数学では群論という分野になっています。