直線の長さが無限とは：ルベーグ測度による説明

どうも、木村（@kimu3_slime）です。

中学校で学ぶ幾何学、ユークリッド幾何学では、「直線」は未定義語ですが、無限に真っすぐ伸びたものとして説明されます。

今回は、直線の長さが無限大とはどういうことか、そのルベーグ測度による大きさが無限であることを紹介します。

直線を数直線、つまり実数と同一視して考えましょう。

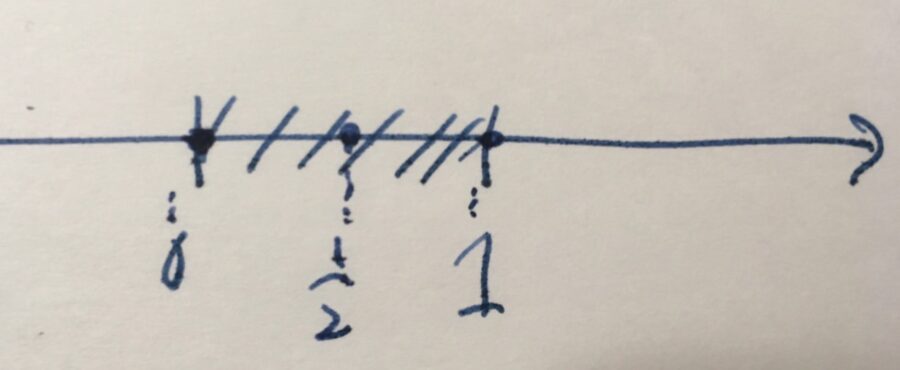
直線の長さは、ルベーグ測度というもので説明されます。1次元のルベーグ測度\(\mu\)は、

\[\mu((a,b)) = b-a\]

を満たします。例えば、開区間（線分）\((0,1) =\{x \mid 0< x < 1\}\)の測度（長さ）は\(\mu ((0,1))= 1-0 =1\)です。

この定義は、考える区間（線分）が有限でなくても成りたちます。

直線とは、実数全体の集まりのことであり、それは\(\mathbb{R} = (-\infty , \infty)=\{x \mid -\infty < x < \infty\}\)として表せます。したがって、さきほどの性質から、直線の長さは

\[\begin{aligned} \mu((-\infty,\infty)) &= \infty+\infty\\&= \infty \end{aligned} \]

と求めることができます。（測度の議論において、無限大同士の和は無限大と定義されています。これは不定形ではありません。）

この議論を見ただけだと、「直線の長さが無限大であるように測り（ルベーグ測度）を用意した」ように見えるかもしれません（それも間違った見方ではないですが）。

長さの単調性という、別の観点からも直線の長さが無限大であると導くことができます。

長さ（測度）には、

単調性：\(A \subset B\)ならば、\(\mu(A )\subset \mu (B)\)

という性質があります。つまり、より多くの要素を持つ集合のほうがより長いと考えるわけです。

例えば、0以上1以下の数の集まり（線分）\((0,1)\)と、0以上5以下の数の集まり\((0,5)\)を比較すると、前者は後者の一部分です\((0,1) \subset (0,5)\)。したがって、その大きさは\(\mu((0,1)) \leq \mu((0,5)) \)と考えることができます。

この議論を直線、すなわち実数全体\(\mathbb{R}\)に当てはめてみましょう。

実数は、あらゆる実数の部分集合より大きいです。\((0,1) \subset \mathbb{R}\)ですし、\((0,5) \subset \mathbb{R}\)ですし、どんなに大きな整数\(n\)に対しても、\((0,n) \subset \mathbb{R}\)です。

つまり、どんなに大きな整数\(n\)に対しても

\[\mu((0,n)) \leq \mu (\mathbb{R})\]

となるわけですが、左辺の長さは\(n\)です。

\[n \leq \mu (\mathbb{R})\]

これは直線の長さが、どんなに大きな整数\(n\)を考えても、それより長いことを意味しています。

これは実数全体（直線）の長さが無限大という結論を導きます。仮にその長さが有限であったとしましょう。その長さを\(L\)としても、\(L\)より大きな整数\(n\)を考えることができます。しかしさきほどの議論から、\(n \leq L\)が成り立つので、これは矛盾します。背理法より、直線の長さは無限大です。

極限の知識を使ってもっと直接的に言えば、

\[n \leq \mu (\mathbb{R})\]

において両辺で\(n\to \infty\)の極限を取ると、極限操作で不等式が保たれること（追い出しの原理）から、

\[\mu (\mathbb{R}) =\lim_{n\to \infty}\mu (\mathbb{R}) =\infty\]

となり、直線の長さが無限大となることがわかりました。

片方に限界がある半直線\((0,\infty)\)などを考えても、同様の議論によってその長さは無限大となります。

今回は簡単のために1次元ルベーグ測度（長さ）を考えましたが、2次元（面積）や3次元（体積）、一般的な次元のルベーグ測度においても、平面や空間全体の測度（大きさ）は無限大となります。

以上、直線の長さが無限とはどういうことか、ルベーグ測度による説明をしてきました。

長さという概念は、長さ同士で比較することができる性質を持っています。直線を考えると、それはどんなに大きい有限の長さを持つ線分をも、部分として含んでいます。したがって、その直線は有限の長さではありえない、無限に大きいと考えられるわけですね。

今回の話において、直線は幾何学上・数学上の概念（モデル）であり、現実に無限の長さの直線が引けるかどうかの話とは別物です。そのモデルにおいて、どうやって無限の長さの「直線」なるものを考えているか、どうして無限となるのかが伝われば嬉しいです。

木村すらいむ（@kimu3_slime）でした。ではでは。