どうも、木村(@kimu3_slime)です。
数学の金融への応用として身近な話といえば、金利の計算でしょう。
漫画「賭博黙示録 カイジ」では、10分3割の複利というとんでもない暴利の貸付が登場します。もちろん現実には違法です。
金利によっていかに利子が大きくなっていくかを感じるために、実際に計算してみましょう。
10分3割の複利計算
最初に借りる金額を元本と呼びます。
元本が1000万円で、利子率が3割ならば、10分後には元本と金利(元利)の合計はいくらでしょうか。1000万円の3割は300万円なので、1300万円となります。
利子のタイプは主に2種類あり、単利と複利があります。
単利ならば、まだ増加のペースはやさしいです。利子の対象となるのは、元本のみです。10分3割ならば、300万ずつ増えていきます。
| 分 | 10 | 20 | 30 | 40 |
| 元利合計(万) | 1300 | 1600 | 1900 | 2200 |
元利を\(a\)、利子率を\(r\)、利子のついた回数を\(n\)とするならば、元利合計は
\[a+ n ar = a(1+nr)\]
となります。いわゆる直線的、1次関数的な増加です。
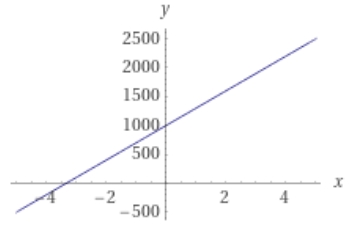
画像引用:WolframAlpha
複利の場合は、元本と利子の両方に利子をかけて計算します。つまり、10分では130万ですが、20分では130万の3割、39万の利子が加わって169万となります。
一般的な元利合計\(b_n\)を計算してみましょう。数列の考え方を用いると便利です。
\[b_0 =a\]
\[b_1 = a+ ar = a(1+r)\]
\[b_2 = b_1+rb_1 = a(1+r)^2\]
というペースで増えていきます。つまり、一般的には
\[b_n = a(1+r)^n\]
という和の合計になります。この数列は、等比数列と呼ばれています。関数の言葉で言えば、指数関数的に、倍々ゲーム的に増加していくものです。
今回の元本と金利ならば、\(b_n = 1000\times 1.3^n\)ですね。
| 分 | 10 | 20 | 30 | 40 |
| 元利合計(万) | 1300 | 1690 | 2197 | 2856 |
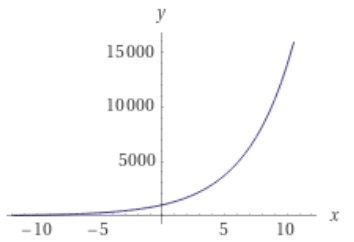
画像引用:WolframAlpha
「賭博黙示録 カイジ」では、元本1000万で10分3割複利で借りて、92分過ぎた後の返済のシーンがあります。これを10回利子が発生したとして計算すると、
\[1000\times 1.3^{10}\simeq 13785.8492\]
と、約1.4億円の元利になることがわかりました。作中では元金1000万を既に払っていたので、1億2875万の支払いが必要になっていましたね。
複利の場合、期間が増えると元利が小さくてもとんでもない金額に膨れ上がります。
1円を10分3割の複利で借りることに同意し、忘れて1年経ってしまったらどうなるでしょうか?(もちろん現実には違法なので無効になりますが)
1年は525600分です。つまり、元利合計は
\[1\times (1.3)^{52560}\simeq 10^{5988}\]
となります。
国家予算規模の1兆円\(10^{12}\)が霞んで小さく見えるほど莫大な金額です。観測可能な宇宙の中にある基本粒子の数は\(10^{80}\)程度、Googleの語源となった巨大な数グーゴル\(10^{100}\)と比べても大きすぎますね(笑)。
以上、金利の数学について、10分3割の複利を計算する方法を紹介してきました。
借金は場合によって便利なものですが、金利を甘く見ると痛い目を見ます。元利の膨らみ方を考えるために、等比数列的に増えるケースを知っておくと良いでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
フクモトプロ/highstone, Inc. (2013-07-25T00:00:00.000Z)
¥396