どうも、木村(@kimu3_slime)です。
学校によっては、しばしば三角関数の関係式を覚えなければならないようです。
高校に通ってる妹の教科書見たんだけど、高校って三角関数のこの程度の関係性も公式扱いして暗記させられるらしい
理屈で想像したらこんなもん暗記しなくてもすぐにわかる筈なのに、そういうのは不要でとりあえず暗記させられるんだからそりゃあ高校生が三角関数嫌いになるわけだわ pic.twitter.com/X7VvP9xFQ7— やべ@やべえ (@cubeym0520) June 24, 2018
これらをいわゆる「公式(文字の羅列)」として覚えていたら、キリがありません。
きちんと導くならば、三角関数の定義(単位円)か、加法定理を使うでしょう。それを知っておくのが基本ですが、毎回検証すると少し面倒くさいです。
そこで今回は、これら関係式の意味を知り、当たり前のものだと思えるように、グラフを描いて考えることを紹介します。
sin、cosの関係式
sinとcosは、バラバラの関数でなく、双子のようなものです。

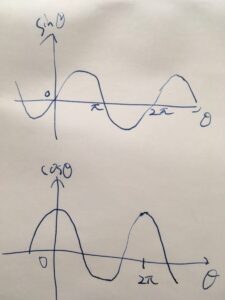
グラフを描いてみましょう。\(\sin \theta\)は、\(\sin 0 =0\)から始まって、山と谷ができて1周期になります。\(\cos \theta\)は、\(\sin \theta\)のグラフを、\(\frac{\pi}{2}\)だけ左にずらしたものです。
周期性
三角関数の重要な性質は、同じ形が繰り返し表れること、周期性です。それを表すのが、
\[\sin (\theta +2 n \pi) = \sin \theta\]
\[\cos (\theta +2n \pi) = \cos \theta\]
です。\(n\)という文字がわかりにくければ、\(\sin (\theta +2 \pi) ,\sin (\theta +4\pi), \sin (\theta -2\pi)\)と具体的な数をあてはめて考えてみて下さい。
グラフを見れば、\(2\pi\)が周期であることがわかります(そうであるようにグラフを描きましょう)。\(2\pi\)が周期であるとは、グラフを横に\(2\pi\)だけずらしても同じ値を取る、\(\sin (\theta + 2\pi) = \sin \theta\)ということです。
\(\sin \theta\)の周期は\(2\pi\)です。ただし、\(\sin 2\theta ,\sin 3 \theta\)の周期は\(2\pi\)ではなくなることに注意しましょう。
対称性
三角関数の原点を中心とした対称性について考えると、
\[\sin (-\theta) = -\sin \theta \]
\[\cos (-\theta) = \cos \theta\]
が成り立つことに気づきます。
\(\sin \theta\)は、原点付近では1次関数\(y =x\)に似ていて、原点付近の右側で正の値を取り、左側で同じ大きさの負の値を取っています。これを表すのが\(\sin (-\theta)= -\sin \theta \)です。
一般に、\(f(-x)= -f(x)\)を満たす関数、原点について点対称な関数を、奇関数と呼びます。1次関数やsinは奇関数です。
\(\cos \theta\)は、原点付近では2次関数\(y=-x^2 \)に似ていて、右側と左側で等しい値を取っています。これを表すのが\(\cos (-\theta)= \cos \theta \)です。
一般に、\(f(-x)=f(x)\)を満たす関数、\(y\)軸について線対称な関数を、偶関数と呼びます。2次関数やcosは偶関数です。
平行移動
三角関数の平行移動について考えましょう。
\[\sin (\theta +\pi )= -\sin \theta\]
\[\cos(\theta +\pi)= -\cos \theta\]
一般に、\(a>0\)として、\(f(x+a)\)は\(f(x)\)を左側に\(a\)だけ並行移動したグラフです。
グラフを\(\pi\)だけ左に動かすと、ちょうど山が谷に、谷が山に重なります。つまり、\(\theta\)軸(横軸)についてグラフを上下に折り返せば、グラフの符号を反転させれば重なる形ということです。
続いて、\(\frac{\pi}{2}\)だけグラフを左に動かすことを考えましょう。今回は、sinがsinに、cosがcosに対応するわけではありません。そこでsinならばcos、cosならばsinのグラフと見比べると、次の関係が成り立っていることがわかりますね。
\[\sin (\theta +\frac{\pi}{2} )= \cos \theta\]
\[\cos(\theta +\frac{\pi}{2})= -\sin \theta\]
sin、cosは\(\frac{\pi}{2}\)だけずらして符号を調整すれば同じ、双子の関係というわけです。
\(\sin (-\theta), \cos (-\theta)\)の平行移動も、同様に考えて導けます。まずグラフを描き、その後平行移動するとどうなっているかを見れば良いです。
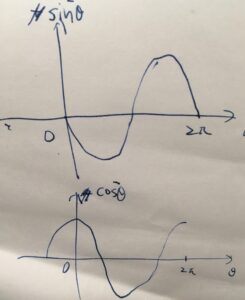
一般に、\(a>0\)として、\(f(-x+a)\)は\(f(-x)\)を右側に\(a\)だけ並行移動したグラフです。
右に\(\pi\)だけずらすと、\(\sin(-\theta)\)は\(\sin \theta\)に、\(\cos (-\theta)\)は\(-\cos \theta\)に重なります。
\[\sin (-\theta +\pi )= \sin \theta\]
\[\cos(-\theta +\pi)= -\cos \theta\]
右に\(\frac{\pi}{2}\)だけずらすと、\(\sin(-\theta)\)は\(\cos \theta\)に、\(\cos (-\theta)\)は\(\sin \theta\)に重なります。
\[\sin (-\theta +\frac{\pi}{2} )= \cos \theta\]
\[\cos(-\theta +\frac{\pi}{2})= \sin \theta\]
tanの関係式
tanのグラフは、まず\(- \frac{\pi}{2} < \theta < \frac{\pi}{2}\)の範囲で描きましょう。原点を通り、S字を縦に伸ばしたような形です。
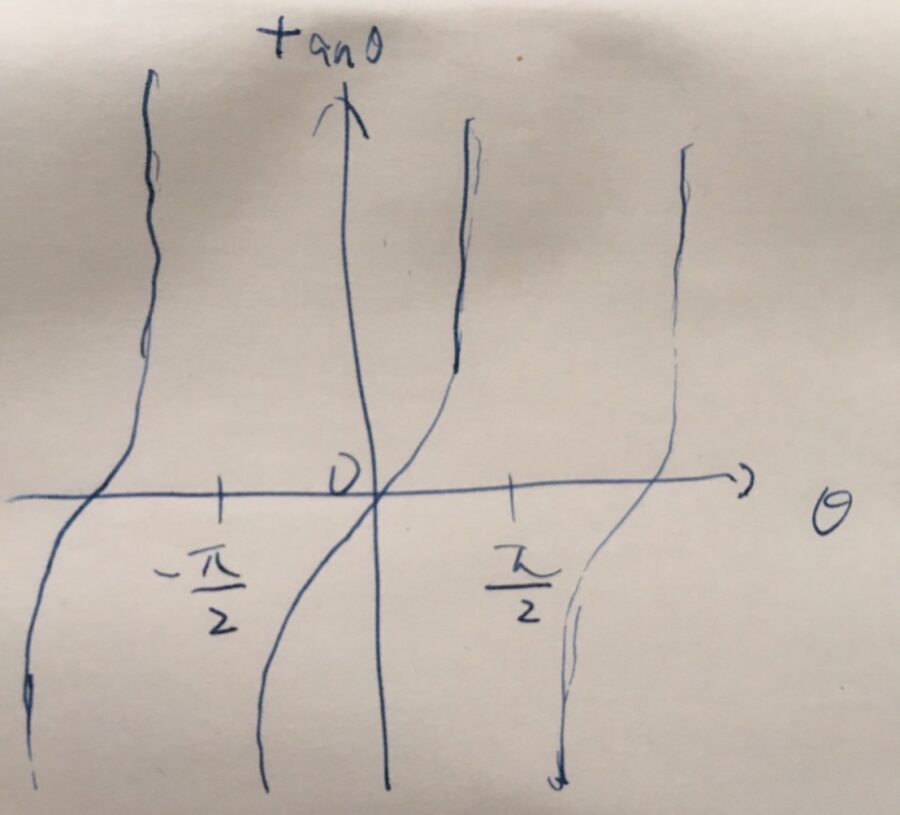
周期性
\(- \frac{\pi}{2} < \theta < \frac{\pi}{2}\)以外の範囲では、これを繰り返した形が並びます(そのようにtanを定義した)。したがって、
\[\tan (\theta +\pi) = \tan \theta\]
\[\tan (\theta +2 n \pi) = \tan \theta\]
が成り立ちます。sin,cosの最小の周期が\(2\pi\)なのに対し、tanの最小の周期は\(\pi\)です。
周期性はsin,cos,tanに共通するもので、三角関数になくてはならない性質です。
対称性
原点付近に注目すると、右側ではプラス、左側ではマイナスで、ちょうど折り返した形になっています。これはsinと似ていて、
\[\tan(-\theta) = -\tan \theta\]
です。つまり、tanは奇関数です。
周期性と対称性を組み合わせれば、
\[\tan(-\theta +\pi) = \tan(-\theta) = -\tan \theta\]
となることもわかりますね。
平行移動
tanは、sin,cosと違って、\(\frac{\pi}{2}\)だけ左に平行移動しても重ならない形をしています。
例えば\(\theta = – \frac{\pi}{3}\)を考えると、\(\tan \theta = -\sqrt{3}\)で、\(\tan (\theta+\frac{\pi}{2}) =\tan \frac{\pi}{6} = \frac{1}{\sqrt{3}}\)です。ここから
\[\tan (\theta +\frac{\pi}{2}) = – \frac{1}{\tan \theta}\]
と予想することはできますね。
\(\theta =\frac{\pi}{6} , \frac{\pi}{3}\)におけるtanの値が逆数になっていること、\(\theta\)の符号を変えるとtanの符号も変わることを知っていれば、この性質は難しくありません。
この形を導くには、tanをsin,cosの比として表し、さきほどの性質を用いるのが簡単でしょう。
\[\begin{aligned} \tan(\theta +\frac{\pi}{2}) &= \frac{\sin(\theta +\frac{\pi}{2})}{\cos (\theta +\frac{\pi}{2})}\\&= \frac{\cos \theta}{ – \sin \theta}\\&=- \frac{1}{\frac{\sin \theta}{\cos \theta}}\\ &= -\frac{1}{\tan \theta}\end{aligned}\]
同様にして、\(\tan (-\theta)\)の平行移動は
\[\begin{aligned} \tan(-\theta +\frac{\pi}{2}) &= \frac{\sin(-\theta +\frac{\pi}{2})}{\cos (-\theta +\frac{\pi}{2})}\\&= \frac{\cos \theta}{ \sin \theta}\\&= \frac{1}{\frac{\sin \theta}{\cos \theta}}\\ &= \frac{1}{\tan \theta}\end{aligned}\]
となりました。
以上、三角関数の性質(周期性、対称性、平行移動)の覚え方について、グラフを描いて考える方法を紹介してきました。
加法定理から導くのは確実ですが、直観的で少し手間がかかります。グラフを描いて公式の意味を知ったり、特殊な値を当てはめて検証すれば、正しい形が何も見ずに推測できるようになるでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
数研出版編集部(著)
数研出版 (2022-02-01T00:00:01Z)
¥1,320 (中古品)